题目内容
11.用配方法解方程(1)2x2-4x-7=0;
(2)3x2-1=6x.
分析 (1)利用配方法得到(x-2)2=$\frac{9}{2}$,然后利用直接开平方法解方程;
(2)利用配方法得到(x-1)2=$\frac{4}{3}$,然后利用直接开平方法解方程.
解答 解:(1)x2-2x=$\frac{7}{2}$,
x2-2x+1=$\frac{7}{2}$+1,
(x-1)2=$\frac{9}{2}$,
x-1=±$\frac{3\sqrt{2}}{2}$,
所以x1=1+$\frac{3\sqrt{2}}{2}$,x2=1-$\frac{3\sqrt{2}}{2}$;
(2)x2-2x=$\frac{1}{3}$,
x2-2x+1=$\frac{1}{3}$+1,
(x-1)2=$\frac{4}{3}$,
x-1=±$\frac{2\sqrt{3}}{3}$,
所以x1=1+$\frac{2\sqrt{3}}{3}$,x2=1-$\frac{2-2\sqrt{3}}{3}$.
点评 本题考查了解一元二次方程-配方法:将一元二次方程配成(x+m)2=n的形式,再利用直接开平方法求解,这种解一元二次方程的方法叫配方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.一块钝角三角形草坪ABC,AB=40m,BC=60m,∠B=120°,若这种草坪每平方米需要m元,则这种草坪共需( )
| A. | 800$\sqrt{3}$m元 | B. | 600$\sqrt{3}$m元 | C. | 1200$\sqrt{3}$m元 | D. | 1200m元 |
8.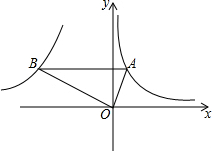 如图,Rt△ABO中,∠AOB=90°,点A在第一象限,点B在第二象限,且AO:BO=1:2,若经过点A的反比例函数解析式为y=$\frac{1}{x}$,则经过点B(x,y)的反比例函数解析式为( )
如图,Rt△ABO中,∠AOB=90°,点A在第一象限,点B在第二象限,且AO:BO=1:2,若经过点A的反比例函数解析式为y=$\frac{1}{x}$,则经过点B(x,y)的反比例函数解析式为( )
 如图,Rt△ABO中,∠AOB=90°,点A在第一象限,点B在第二象限,且AO:BO=1:2,若经过点A的反比例函数解析式为y=$\frac{1}{x}$,则经过点B(x,y)的反比例函数解析式为( )
如图,Rt△ABO中,∠AOB=90°,点A在第一象限,点B在第二象限,且AO:BO=1:2,若经过点A的反比例函数解析式为y=$\frac{1}{x}$,则经过点B(x,y)的反比例函数解析式为( )| A. | y=$\frac{2}{x}$ | B. | y=-$\frac{2}{x}$ | C. | y=-$\frac{4}{x}$ | D. | y=-$\frac{8}{x}$ |
 如图,矩形OABC在平面直角坐标系中,A、C两点的坐标分别为A(6,0),C(0,-3),直线y=-$\frac{3}{4}$x与BC边相交于D点,过原点的抛物线y=ax2+bx经过A、D两点.
如图,矩形OABC在平面直角坐标系中,A、C两点的坐标分别为A(6,0),C(0,-3),直线y=-$\frac{3}{4}$x与BC边相交于D点,过原点的抛物线y=ax2+bx经过A、D两点. 如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC=2,O为AC中点,若点D在直线BC上运动,连接OE,则在点D运动过程中,线段OE的最小值是为$\frac{\sqrt{2}}{2}$.
如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC=2,O为AC中点,若点D在直线BC上运动,连接OE,则在点D运动过程中,线段OE的最小值是为$\frac{\sqrt{2}}{2}$.