题目内容
15.已知反比例函数y=-$\frac{{a}^{2}+{b}^{2}}{x}$的图象上有三个点(x1,y1),(x2,y2)、(x3,y3),且x1<x2<0<x3,则y1、y2、y3的大小关系是( )| A. | y1>y2>y3 | B. | y2>y1>y3 | C. | y3>y1>y2 | D. | y3>y2>y1 |
分析 根据函数的解析式得出图象所在的象限和增减性,再进行比较即可.
解答 解:∵反比例函数y=-$\frac{{a}^{2}+{b}^{2}}{x}$,
∴函数图象在第二、四象限,且在每个象限内,y随x的增大而增大,
∵函数的图象上有三个点(x1,y1),(x2,y2)、(x3,y3),且x1<x2<0<x3,
∴y2>y1>y3,
故选B.
点评 本题考查了反比例函数图象上点的坐标特征和函数的图象和性质,能灵活运用函数的图象和性质进行推理是解此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.一批面粉,标准质量为每袋25kg,质监部门抽取10袋样品进行检测,把超过标准质量的千克数用正数表示,不足的用负数表示,结果如表:
求这10袋面粉质量的平均数.
| 袋号 | 1 | 2 | 3 | 4 | 5 |
| 与标准质量的差/kg | +1 | -0.5 | -1.5 | +0.75 | -0.25 |
| 袋号 | 6 | 7 | 8 | 9 | 10 |
| 与标准质量的差/kg | +1.5 | -1 | +0.5 | 0 | +0.5 |
6.已知$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$是关于x的二元一次方程mx+3y=-m的一个解,则m的值是( )
| A. | -1 | B. | 1 | C. | -3 | D. | 3 |
20.将分式$\frac{6m{n}^{3}}{4{m}^{3}n}$化成最简分式的结果正确的是( )
| A. | $\frac{6{n}^{2}}{4{m}^{2}}$ | B. | $\frac{6n}{4m}$ | C. | $\frac{3{n}^{2}}{2{m}^{2}}$ | D. | $\frac{3n}{2m}$ |
4.下列计算结果正确的是( )
| A. | (a3)2=a6 | B. | (-3a2)2=6a4 | C. | (-a2)3=a6 | D. | (-$\frac{1}{2}$ab2)3=$\frac{1}{8}$a3b6 |
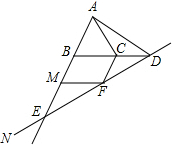 如图,在等边△ABC中,点D在BC的延长线上,连接AD,∠ADN=60°,直线DN交射线AB于点E,过点C作CF∥AB交直线DN于点F,过点F作MF∥BC交射线AB于点M.
如图,在等边△ABC中,点D在BC的延长线上,连接AD,∠ADN=60°,直线DN交射线AB于点E,过点C作CF∥AB交直线DN于点F,过点F作MF∥BC交射线AB于点M.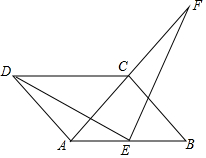 如图,四边形ABCD是平行四边形,AD=AC,AD⊥AC,E是AB的中点,F是AC延长线上的一点.
如图,四边形ABCD是平行四边形,AD=AC,AD⊥AC,E是AB的中点,F是AC延长线上的一点.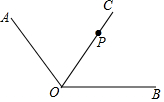 如图,已知OC平分∠AOB,点P是OC上一点,作图:过点P画PE⊥OA,PF⊥OB,垂足分别为点E和点F,并完成填空:PE=PF(填“>”或“=”“<”).
如图,已知OC平分∠AOB,点P是OC上一点,作图:过点P画PE⊥OA,PF⊥OB,垂足分别为点E和点F,并完成填空:PE=PF(填“>”或“=”“<”).