题目内容
7.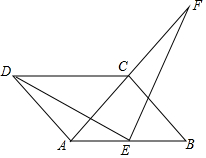 如图,四边形ABCD是平行四边形,AD=AC,AD⊥AC,E是AB的中点,F是AC延长线上的一点.
如图,四边形ABCD是平行四边形,AD=AC,AD⊥AC,E是AB的中点,F是AC延长线上的一点.(1)若ED⊥EF,求证:ED=EF;
(2)在(1)的条件下,若DC的延长线与FB交于点P,试判断四边形ACPE是否为平行四边形?并证明你的结论(请先补全图形,再解答);
(3)在(1)的条件下,若BC的延长线交DF于点Q,连接QA与QE.试说明QA=QE.
分析 (1)根据平行四边形的想知道的AD=AC,AD⊥AC,连接CE,根据全等三角形的判定和性质即可得到结论;
(2)根据全等三角形的性质得到CF=AD,等量代换得到AC=CF,于是得到CP=$\frac{1}{2}$AB=AE,根据平行四边形的判定定理即可得到四边形ACPE为平行四边形;
(3)由(1)知AC=CF,根据三角形的中位线的性质得到DQ=FQ,根据直角三角形的性质即可得到结论.
解答 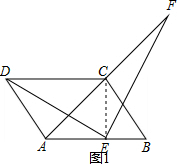 (1)证明:在?ABCD中,
(1)证明:在?ABCD中,
∵AD=AC,AD⊥AC,
∴AC=BC,AC⊥BC,
连接CE,
∵E是AB的中点,
∴AE=EC,CE⊥AB,
∴∠ACE=∠BCE=45°,
∴∠ECF=∠EAD=135°,
∵ED⊥EF,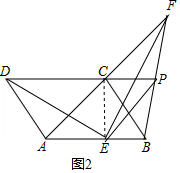
∴∠CEF=∠AED=90°-∠CED,
在△CEF和△AED中,$\left\{\begin{array}{l}{∠CEF=∠AED}\\{EC=AE}\\{∠ECF=∠EAD}\end{array}\right.$,
∴△CEF≌△AED,
∴ED=EF;
(2)解:由(1)知△CEF≌△AED,CF=AD,
∵AD=AC,
∴AC=CF,
∵DP∥AB,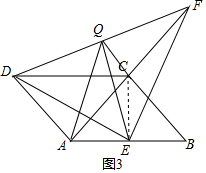
∴FP=PB,
∴CP=$\frac{1}{2}$AB=AE,
∴四边形ACPE为平行四边形;
(3)由(1)知AC=CF,
∵CQ∥AD,
∴DQ=FQ,
∵在Rt△DAF与Rt△DEF中,
∴AQ=EQ=$\frac{1}{2}$DF.
点评 本题考查了平行四边形的性质和判定,全等三角形的判定和性质,等腰直角三角形的性质,正确的作出辅助线是解题的关键.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
15.已知反比例函数y=-$\frac{{a}^{2}+{b}^{2}}{x}$的图象上有三个点(x1,y1),(x2,y2)、(x3,y3),且x1<x2<0<x3,则y1、y2、y3的大小关系是( )
| A. | y1>y2>y3 | B. | y2>y1>y3 | C. | y3>y1>y2 | D. | y3>y2>y1 |
17.若$\sqrt{10201}$=101,则$\sqrt{102.01}$等于( )
| A. | 1.01 | B. | 10.1 | C. | 101 | D. | 1.0201 |
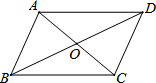 如图,从下列四个条件①AB=BC,②AC⊥BD,③∠ABC=90°,④AC=BD中选两个作为补充条件,使?ABCD成为正方形,下列四种选法错误的是( )
如图,从下列四个条件①AB=BC,②AC⊥BD,③∠ABC=90°,④AC=BD中选两个作为补充条件,使?ABCD成为正方形,下列四种选法错误的是( )


