题目内容
10.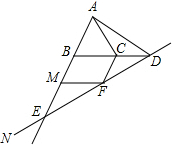 如图,在等边△ABC中,点D在BC的延长线上,连接AD,∠ADN=60°,直线DN交射线AB于点E,过点C作CF∥AB交直线DN于点F,过点F作MF∥BC交射线AB于点M.
如图,在等边△ABC中,点D在BC的延长线上,连接AD,∠ADN=60°,直线DN交射线AB于点E,过点C作CF∥AB交直线DN于点F,过点F作MF∥BC交射线AB于点M.(1)四边形BCFM是平行四边形吗?请说明理由;
(2)求证:CF+CD=BE;
(3)若∠ADC=30°,AB=8,求BE、CD的长.
分析 (1)根据平行四边形的判定定理即可得到结论;
(2)由四边形BCFM是平行四边形,得到BM=CF,FM=BC,由△ABC是等边三角形,得到AC=BC,∠ACB=∠ABC=60°,等量代换得到AC=MF,根据全等三角形的性质即可得到结论;
(3)由∠ADC=30°,∠ACB=∠ABC=60°,得到∠BAD=90°,∠CAD=∠CDA=30°,根据等腰三角形的判定和性质即可得到结论.
解答 解:(1)四边形BCFM是平行四边形,
理由:∵CF∥AB,MF∥BC,
∴四边形BCFM是平行四边形;
(2)∵四边形BCFM是平行四边形,
∴BM=CF,FM=BC,
∵△ABC是等边三角形,
∴AC=BC,∠ACB=∠ABC=60°,
∴AC=MF,
∵MF=BC,
∴∠BMF=∠ABC=60°,∠CDF=∠MFE,
∴∠ACD=∠EMF=120°,
∴∠MEF+∠MFE=60°,
∵∠ADN=60°,
∴∠ADC+∠CDF=60°,
∴∠ADC=∠MEF,
在△ACD与△FME中,$\left\{\begin{array}{l}{∠ADC=∠MEF}\\{∠ACD=∠EMF}\\{AC=MF}\end{array}\right.$,
∴△ACD≌△FME,
∴CD=ME,
∴BE=BM+ME=CF+CD;
(3)∵∠ADC=30°,∠ACB=∠ABC=60°,
∴∠BAD=90°,∠CAD=∠CDA=30°,∠BDE=30°,
∵AB=8,
∴BD=16,AC=AB=BC=8,
∴CD=AC=8,
∵∠BDE=30°,∠EBD=120°,
∴∠BED=∠BDE=30°,
∴BE=BD=16.
点评 本题考查了平行四边形的判定和性质,全等三角形的判定和性质,等腰三角形的性质,熟练掌握平行四边形的判定和性质是解题的关键.

 快捷英语周周练系列答案
快捷英语周周练系列答案| A. | y1>y2>y3 | B. | y2>y1>y3 | C. | y3>y1>y2 | D. | y3>y2>y1 |
 如图,已知线段AB,请按要求完成下列问题.
如图,已知线段AB,请按要求完成下列问题.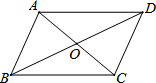 如图,从下列四个条件①AB=BC,②AC⊥BD,③∠ABC=90°,④AC=BD中选两个作为补充条件,使?ABCD成为正方形,下列四种选法错误的是( )
如图,从下列四个条件①AB=BC,②AC⊥BD,③∠ABC=90°,④AC=BD中选两个作为补充条件,使?ABCD成为正方形,下列四种选法错误的是( )



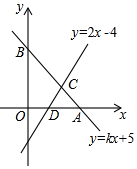 已知直线y=kx+5交x轴于A,交y轴于B且A坐标为(5,0),直线y=2x-4与x轴于D,与直线AB相交于点C.
已知直线y=kx+5交x轴于A,交y轴于B且A坐标为(5,0),直线y=2x-4与x轴于D,与直线AB相交于点C.