题目内容
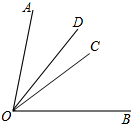
 如图,A、O、E三点在同一直线上,∠DOE=20°,OB平分∠AOC,且∠COD:∠BOC=2:3,求∠AOC的度数.
如图,A、O、E三点在同一直线上,∠DOE=20°,OB平分∠AOC,且∠COD:∠BOC=2:3,求∠AOC的度数.考点:角平分线的定义
专题:
分析:首先根据角平分线的性质可得∠AOC=2∠BOC=2∠AOB,然后再由条件∠DOE=20°,可得∠AOD=160°,再设∠COD=2x°,则∠BOC=3x°,∠AOB=3x°,利用方程计算出x,进而可得∠AOC的度数.
解答:解:∵OB平分∠AOC,
∴∠AOC=2∠BOC=2∠AOB,
∵∠DOE=20°,
∴∠AOD=160°,
∵∠COD:∠BOC=2:3,
∴设∠COD=2x°,则∠BOC=3x°,∠AOB=3x°,
∴2x+3x+3x=160,
解得:x=20,
∴∠AOC=6×20°=120°.
∴∠AOC=2∠BOC=2∠AOB,
∵∠DOE=20°,
∴∠AOD=160°,
∵∠COD:∠BOC=2:3,
∴设∠COD=2x°,则∠BOC=3x°,∠AOB=3x°,
∴2x+3x+3x=160,
解得:x=20,
∴∠AOC=6×20°=120°.
点评:此题主要考查了角平分线,关键是掌握方程思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列说法正确的是( )
A、“掷一枚硬币正面朝上的概率是
| ||
| B、一组数据2,2,3,6的众数和中位数都是2 | ||
| C、要了解全市人民的低碳生活状况,适宜采用抽样调查的方法 | ||
| D、随机抽取甲、乙两名同学的5次数学成绩,计算得平均分都是90分,方差分别是S2甲=5,S2乙=12,说明乙的成绩较为稳定 |
 已知:如图,OC平分∠AOB,OD与OC不重合且在∠AOC内部,求证:∠DOC=
已知:如图,OC平分∠AOB,OD与OC不重合且在∠AOC内部,求证:∠DOC= 如图是一个包装纸盒的三视图(单位cm),则制作一个纸盒所需纸板的面积是多少?
如图是一个包装纸盒的三视图(单位cm),则制作一个纸盒所需纸板的面积是多少?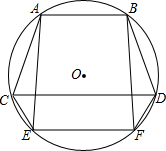 如图,AB,CD,EF为⊙O的弦,AB∥CD∥EF,求证:△ACE≌△BDF.
如图,AB,CD,EF为⊙O的弦,AB∥CD∥EF,求证:△ACE≌△BDF. 如图,一次函数y=ax+b的图象与反比例函数y=
如图,一次函数y=ax+b的图象与反比例函数y=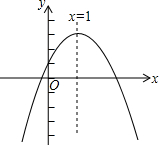 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论: