题目内容
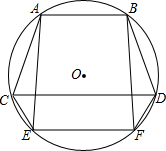如图，AB，CD，EF为⊙O的弦，AB∥CD∥EF，求证：△ACE≌△BDF．考点：全等三角形的判定,圆周角定理
专题：证明题
分析：根据AB∥CD∥EF，可得
=
，
=
，
=
，进而得到AC=BD，CE=DF，AE=BF，根据SSS定理可判定△ACE≌△BDF．
 |
| AC |
|
| DB |
|
| CE |
|
| DF |
|
| ACE |
|
| BDF |
解答：证明：∵AB∥CD∥EF，
∴
=
，
=
，
=
，
∴AC=BD，CE=DF，AE=BF，
在△ACE和△BDF中，
，
∴△ACE≌△BDF（SSS）．
∴
|
| AC |
|
| DB |
|
| CE |
|
| DF |
|
| ACE |
|
| BDF |
∴AC=BD，CE=DF，AE=BF，
在△ACE和△BDF中，
|
∴△ACE≌△BDF（SSS）．
点评：此题主要考查了圆周角定理，以及全等三角形的判定，关键是证明AC=BD，CE=DF，AE=BF．
练习册系列答案
相关题目
在△ABC与△A′B′C′中，AB：AC=A′B′：A′C′，∠B=∠B′，则这两个三角形（ ）
| A、相似，但不全等 |
| B、全等或相似 |
| C、不相似 |
| D、无法判断是否相似 |
如图：
如图，A、O、E三点在同一直线上，∠DOE=20°，OB平分∠AOC，且∠COD：∠BOC=2：3，求∠AOC的度数．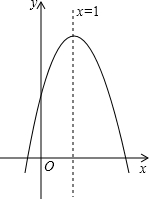
二次函数y=ax2+bx+c（a≠0）的图象如图所示，对于下列结论：①a＜0；②b＜0；③c＞0；④2a+b=0；⑤a-b+c＜0，其中正确的个数是（ ）