题目内容
2.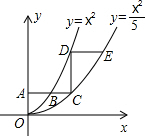 如图,平行于x轴的直线AC分别交抛物线y1=x2(x≥0)与y2=$\frac{{x}^{2}}{5}$(x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则$\frac{DE}{AB}$=5-$\sqrt{5}$.
如图,平行于x轴的直线AC分别交抛物线y1=x2(x≥0)与y2=$\frac{{x}^{2}}{5}$(x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则$\frac{DE}{AB}$=5-$\sqrt{5}$.
分析 设A点坐标为(0,a),利用两个函数解析式求出点B、C的坐标,然后求出BC的长度,再根据CD∥y轴,利用y1的解析式求出D点的坐标,然后利用y2求出点E的坐标,从而得到DE的长度,然后求出比值即可得解.
解答 解:设A点坐标为(0,a),(a>0),
则x2=a,解得x=$\sqrt{a}$,
∴点B($\sqrt{a}$,a),$\frac{{x}^{2}}{5}$=a,
则x=$\sqrt{5a}$,
∴点C($\sqrt{5a}$,a),
∴BC=$\sqrt{5a}$-$\sqrt{a}$.
∵CD∥y轴,
∴点D的横坐标与点C的横坐标相同,为$\sqrt{5a}$,
∴y1=($\sqrt{5a}$)2=5a,
∴点D的坐标为($\sqrt{5a}$,5a).
∵DE∥AC,
∴点E的纵坐标为5a,
∴$\frac{{x}^{2}}{5}$=5a,
∴x=5$\sqrt{a}$,
∴点E的坐标为(5$\sqrt{a}$,5a),
∴DE=5$\sqrt{a}$-$\sqrt{5a}$,
∴$\frac{DE}{AB}$=$\frac{5\sqrt{a}-\sqrt{5a}}{\sqrt{a}}$=5-$\sqrt{5}$.
故答案是:5-$\sqrt{5}$.
点评 本题是二次函数综合题型,主要利用了二次函数图象上点的坐标特征,根据平行与x轴的点的纵坐标相同,平行于y轴的点的横坐标相同,求出用点A的纵坐标表示出各点的坐标是解题的关键.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
12.下列各运算中,计算正确的是( )
| A. | 2a•3a=6a | B. | a4÷a2=2 | C. | (2a2)3=8a6 | D. | (a+b)2=a2+b2 |
10.3x=4y(xy≠0),则下列各式中不成立的( )
| A. | $\frac{x+y}{y}$=$\frac{7}{3}$ | B. | $\frac{x-y}{y}$=$\frac{1}{3}$ | C. | $\frac{x}{x-y}$=4 | D. | $\frac{x+1}{y+1}$=$\frac{5}{4}$ |
7.在数轴上有一个点A在点-2.5的左边3个单位处,则点A所表示的数是( )
| A. | -0.5 | B. | -5.5 | C. | 0.5 | D. | 5.5 |
11.若y=$\frac{1}{\sqrt{4-x}}$有意义,则x的取值范围是( )
| A. | x≠4 | B. | x≤4 | C. | x≥4 | D. | x<4 |