题目内容
10.3x=4y(xy≠0),则下列各式中不成立的( )| A. | $\frac{x+y}{y}$=$\frac{7}{3}$ | B. | $\frac{x-y}{y}$=$\frac{1}{3}$ | C. | $\frac{x}{x-y}$=4 | D. | $\frac{x+1}{y+1}$=$\frac{5}{4}$ |
分析 根据等式的性质,可得$\frac{x}{y}$,根据和比性质,分比性质,反比性质,可得答案.
解答 解:3x=4y,得
$\frac{x-y}{y}$=$\frac{4-3}{3}$=$\frac{1}{3}$,$\frac{x}{y}$=$\frac{4}{3}$.
A、由和比性质,得$\frac{x+y}{y}$=$\frac{4+3}{3}$=$\frac{7}{3}$,故A正确;
B、由分比性质,得$\frac{x-y}{y}$=$\frac{4-3}{3}$=$\frac{1}{3}$,故B正确;
C、由3x=4y,得$\frac{y}{x}$=$\frac{3}{4}$,由$\frac{x-y}{x}$=$\frac{4-3}{4}$=$\frac{1}{4}$,$\frac{x}{x-y}$=4,故C正确;
D、$\frac{x}{y}$=$\frac{4}{3}$,分子分母都加同一个数,分数的值发生变化,故D错误;
故选:D.
点评 本题考查了比例的性质,利用了和比性质,分比性质反比性质,分式的性质.

练习册系列答案
相关题目
20.某种商品原价为100元,经过两次降价后,现价为64元/件,这两次降价中平均每次降价的百分率为( )
| A. | 10% | B. | 18% | C. | 20% | D. | 36% |
5.抛物线y=4(x-3)2+7的顶点坐标是( )
| A. | (3,7) | B. | (-3,7) | C. | (3,-7) | D. | (-3,-7) |
20.下列各数:-5,2,-3,1,$\frac{1}{2}$中,正整数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,AB、AC是⊙O的两条切线,切点分别为B、C,D是优弧$\widehat{BC}$上的一点,已知∠BAC=80°,那么∠BDC=( )度.
如图,AB、AC是⊙O的两条切线,切点分别为B、C,D是优弧$\widehat{BC}$上的一点,已知∠BAC=80°,那么∠BDC=( )度.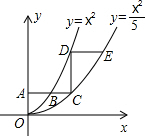 如图,平行于x轴的直线AC分别交抛物线y1=x2(x≥0)与y2=$\frac{{x}^{2}}{5}$(x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则$\frac{DE}{AB}$=5-$\sqrt{5}$.
如图,平行于x轴的直线AC分别交抛物线y1=x2(x≥0)与y2=$\frac{{x}^{2}}{5}$(x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则$\frac{DE}{AB}$=5-$\sqrt{5}$.