题目内容
如图，在5×4正方形网格中，有A，B，C三个格点．试在图中再找出一个格点D，满足：D与A，B，C三点中的两点组成的三角形恰好与△ABC相似．请找出三种不同方案画出符合题意的三角形，并写出所画三角形与△ABC的面积比．考点：作图—相似变换
专题：
分析：分别根据相似三角形的判定与性质得出符合题意的三角形，再利用相似三角形的面积比等于相似比的平方得出即可．
解答：解：如图1所示：
△ABD∽△BCA，
S△ABD：S△BCA=（
） 2=1：5；
如图2所示：
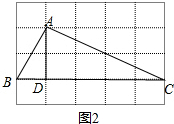
∵△ABD∽△CBA，
∴S△ABD：S△CBA=（
） 2=1：5；
∵△ADC∽△BAC，
∴S△ADC：S△BAC=（
） 2=4：5；
如图3所示：
∵△BDC≌△CAB，
∴S△BDC：S△CAB=1：1；
如图4所示：
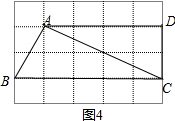
∵△ACD∽△CBA，
∴S△ACD：S△CBA=（
） 2=4：5．
△ABD∽△BCA，
S△ABD：S△BCA=（
| 1 | ||
|
如图2所示：
∵△ABD∽△CBA，
∴S△ABD：S△CBA=（
| 1 | ||
|
∵△ADC∽△BAC，
∴S△ADC：S△BAC=（
| 2 | ||
|
如图3所示：
∵△BDC≌△CAB，
∴S△BDC：S△CAB=1：1；
如图4所示：
∵△ACD∽△CBA，
∴S△ACD：S△CBA=（
| 2 | ||
|
点评：此题主要考查了相似三角形的判定与性质以及面积比与对应边比的关系，正确根据对应边相等的三角形是相似三角形得出是解题关键．
练习册系列答案
相关题目
关于x的一元二次方程x2+2ax+（a2+1）=0的根的情况说法正确的是（ ）
| A、有两个实数根 |
| B、有两个不相等的实数根 |
| C、没有实数根 |
| D、无法确定 |
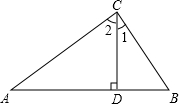如图，△ABC中，CD⊥AB于D，一定能确定△ABC为直角三角形的条件的个数是
如图，在直角梯形ABCD中，AB∥DC，∠A=90°，若DC=3cm，AB=9cm，则此梯形的中位线长为