题目内容
是否存在整数x、y使得y2=x2+2009.
考点:整数问题的综合运用
专题:
分析:首先把y2=x2+2009移项,因式分解为(y-x)(y+x)=2009,再把2009分解为2009=2009×1或-2009×(-1),列出x、y的二元二次方程,求出x、y的值即可.
解答:解:∵y2=x2+2009,
∴(y-x)(y+x)=2009;
∵2009=2009×1或-2009×(-1),
∴
或
或
或
,
解得
或y=
或
或
.
故存在整数x、y使得y2=x2+2009.
∴(y-x)(y+x)=2009;
∵2009=2009×1或-2009×(-1),
∴
|
|
|
|
解得
|
|
|
|
故存在整数x、y使得y2=x2+2009.
点评:本题主要考查整数问题x、y使得y2=x2+2009的综合运用的知识点,解答本题的关键是把2009分解成2009×1或-2009×(-1),此题难度一般.

练习册系列答案
相关题目
 如图,已知圆周角∠BAD=50°,那么圆周角∠BCD的度数为( )
如图,已知圆周角∠BAD=50°,那么圆周角∠BCD的度数为( )| A、130° | B、100° |
| C、50° | D、40° |
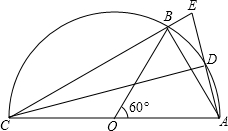 如图,AC是半圆O的直径,B是半圆上的一点,D是弧AB的中点,连接AB、CB、CD、AD,延长AD交CB的延长线于点E.
如图,AC是半圆O的直径,B是半圆上的一点,D是弧AB的中点,连接AB、CB、CD、AD,延长AD交CB的延长线于点E. 已知△ABC在平面直角坐标系xOy中的位置如图所示,△ABC绕点B顺时针旋转90°后得到△A′B′C′.
已知△ABC在平面直角坐标系xOy中的位置如图所示,△ABC绕点B顺时针旋转90°后得到△A′B′C′. 如图,在5×4正方形网格中,有A,B,C三个格点.试在图中再找出一个格点D,满足:D与A,B,C三点中的两点组成的三角形恰好与△ABC相似.请找出三种不同方案画出符合题意的三角形,并写出所画三角形与△ABC的面积比.
如图,在5×4正方形网格中,有A,B,C三个格点.试在图中再找出一个格点D,满足:D与A,B,C三点中的两点组成的三角形恰好与△ABC相似.请找出三种不同方案画出符合题意的三角形,并写出所画三角形与△ABC的面积比.