题目内容
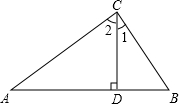 如图,△ABC中,CD⊥AB于D,一定能确定△ABC为直角三角形的条件的个数是
如图,△ABC中,CD⊥AB于D,一定能确定△ABC为直角三角形的条件的个数是①∠1=∠A;②
| CD |
| AD |
| DB |
| CD |
考点:相似三角形的判定与性质
专题:
分析:求出∠2+∠1=∠2+∠A=90°,即可判断①;证△ADC∽△CDB,推出∠A=∠1,即可求出∠ACB=90°,即可判断②,根据已知推出∠2=∠B,不能推出∠1+∠2=90°,即可判断③;根据勾股定理的逆定理即可判断④,根据已知得出比例式,即可判断⑤.
解答:解:①∠1=∠A正确;
∵CD⊥AB,
∴∠ADC=∠BDC=90°,
∴∠2+∠A=90°,
∵∠1=∠A,
∴∠1+∠2=90°,
∴∠ACB=90°,即△ABC是直角三角形;
②正确,
理由是:∵
=
,∠ADC=∠BDC=90°,
∴△ADC∽△CDB,
∴∠A=∠1,
∴∠1+∠2=90°,
∴∠ACB=90°,即△ABC是直角三角形;
③错误,
理由是:∵∠BDC=90°,
∠1+∠B=90°,
∵∠2+∠B=90°,
∴∠1=∠2,不能推出∠1+∠2=90°,∴③错误;
④正确;
∵BC:AC:AB=3:4:5,
∴设BC=3k,AC=4k,AB=5k,
则BC2+AC2=25k2,AB2=25k2,
即BC2+AC2=AB2,
∴∠ACB=90°,即④正确;
⑤正确;
∵AC•BD=BC•CD,
∴
=
,
∵∠ADC=∠BDC=90°,
无法得到△ACB是直角三角形,∴⑤错误;
正确的个数是3个.
故答案为:3个.
∵CD⊥AB,
∴∠ADC=∠BDC=90°,
∴∠2+∠A=90°,
∵∠1=∠A,
∴∠1+∠2=90°,
∴∠ACB=90°,即△ABC是直角三角形;
②正确,
理由是:∵
| CD |
| AD |
| DB |
| CD |
∴△ADC∽△CDB,
∴∠A=∠1,
∴∠1+∠2=90°,
∴∠ACB=90°,即△ABC是直角三角形;
③错误,
理由是:∵∠BDC=90°,
∠1+∠B=90°,
∵∠2+∠B=90°,
∴∠1=∠2,不能推出∠1+∠2=90°,∴③错误;
④正确;
∵BC:AC:AB=3:4:5,
∴设BC=3k,AC=4k,AB=5k,
则BC2+AC2=25k2,AB2=25k2,
即BC2+AC2=AB2,
∴∠ACB=90°,即④正确;
⑤正确;
∵AC•BD=BC•CD,
∴
| AC |
| BC |
| CD |
| DB |
∵∠ADC=∠BDC=90°,
无法得到△ACB是直角三角形,∴⑤错误;
正确的个数是3个.
故答案为:3个.
点评:本题考查了三角形的内角和定理,相似三角形的性质和判定的应用,主要考查学生的推理能力和辨析能力,题目比较好,有一定的难度.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
 已知△ABC在平面直角坐标系xOy中的位置如图所示,△ABC绕点B顺时针旋转90°后得到△A′B′C′.
已知△ABC在平面直角坐标系xOy中的位置如图所示,△ABC绕点B顺时针旋转90°后得到△A′B′C′. 如图,在5×4正方形网格中,有A,B,C三个格点.试在图中再找出一个格点D,满足:D与A,B,C三点中的两点组成的三角形恰好与△ABC相似.请找出三种不同方案画出符合题意的三角形,并写出所画三角形与△ABC的面积比.
如图,在5×4正方形网格中,有A,B,C三个格点.试在图中再找出一个格点D,满足:D与A,B,C三点中的两点组成的三角形恰好与△ABC相似.请找出三种不同方案画出符合题意的三角形,并写出所画三角形与△ABC的面积比. 如图在⊙O中,AC=BC,OD=OE,求证:∠ACD=∠BCE.
如图在⊙O中,AC=BC,OD=OE,求证:∠ACD=∠BCE. 如图,A、B、C都是⊙O上的点,
如图,A、B、C都是⊙O上的点,
 菱形ABCD中,E、F分别为AB、AD的中点.
菱形ABCD中,E、F分别为AB、AD的中点.