Question

1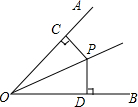．如图，OP为∠AOB的角平分线，PC⊥OA，PD⊥OB，垂足分别是C、D，则下列结论错误的是（　　）

• A． PC=PD
• B． ∠CPD=∠DOP
• C． ∠CPO=∠DPO
• D． OC=OD

Answer 1

分析 先根据角平分线的性质得出PC=PD，再利用HL证明△OCP≌△ODP，根据全等三角形的性质得出∠CPO=∠DPO，OC=OD．

解答 解：∵OP为∠AOB的角平分线，PC⊥OA，PD⊥OB，垂足分别是C、D，
∴PC=PD，故A正确；
在Rt△OCP与Rt△ODP中，
$\left\{\begin{array}{l}{OP=OP}\\{PC=PD}\end{array}\right.$，
∴△OCP≌△ODP，
∴∠CPO=∠DPO，OC=OD，故C、D正确．
不能得出∠CPD=∠DOP，故B错误．
故选B．

点评 本题考查了角平分线的性质：角的平分线上的点到角的两边的距离相等．也考查了全等三角形的判定与性质，得出PC=PD是解题的关键．