题目内容
11. 如图,一次函数y1=kx+b的图象与反比例函数y2=$\frac{a}{x}$的图象相交于A,B两点,直线AB与x轴相交于点C,点B的坐标为(-6,m),线段OA=5,E为x轴正半轴上一点,且cos∠AOE=$\frac{3}{5}$.
如图,一次函数y1=kx+b的图象与反比例函数y2=$\frac{a}{x}$的图象相交于A,B两点,直线AB与x轴相交于点C,点B的坐标为(-6,m),线段OA=5,E为x轴正半轴上一点,且cos∠AOE=$\frac{3}{5}$.(1)求反比例函数的解析式;
(2)求证:S△AOC=2S△BOC;
(3)直接写出当y1>y2时,x的取值范围.
分析 (1)通过解直角三角形求出点A的坐标,进而得出反比例函数解析式;
(2)先根据反比例函数解析式求得点B的坐标,再根据△AOC和△BOC的面积计算公式,即可得出结论;
(3)结合两函数图象,找出反比例函数图象在一次函数图象下方时x的取值范围即可.
解答  解:过点A作AD⊥x轴于点D,
解:过点A作AD⊥x轴于点D,
∵cos∠AOE=$\frac{OD}{5}$=$\frac{3}{5}$,
∴OD=3,
∴AD=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴A(3,4),
将点A的坐标代入反比例函数y2=$\frac{a}{x}$得,a=12,
∴反比例函数解析式为${y}_{2}=\frac{12}{x}$;
(2)将点B(-6,m)代入反比例函数${y}_{2}=\frac{12}{x}$得,m=-2,
∴B(-6,-2),而A(3,4),
∴△AOC的面积=$\frac{1}{2}$×OC×4=2OC,
△BOC的面积=$\frac{1}{2}$×OC×2=OC,
∴S△AOC=2S△BOC;
(3)当y1>y2时,x的取值范围为-6<x<0或x>3.
点评 本题主要考查了反比例函数与一次函数的交点问题,解题的关键是:(1)通过解直角三角形求出点A的坐标,并利用待定系数法求出函数解析式;(2)利用函数图象解不等式.在计算三角形面积时,若三角形的一边与坐标轴平行或垂直,则一般以该边为底边.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.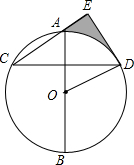 如图,AB是⊙O的直径,弦CD⊥AB,DE⊥CE于E,∠AOD=60°,CD=2$\sqrt{3}$,则S阴影=( )
如图,AB是⊙O的直径,弦CD⊥AB,DE⊥CE于E,∠AOD=60°,CD=2$\sqrt{3}$,则S阴影=( )
 如图,AB是⊙O的直径,弦CD⊥AB,DE⊥CE于E,∠AOD=60°,CD=2$\sqrt{3}$,则S阴影=( )
如图,AB是⊙O的直径,弦CD⊥AB,DE⊥CE于E,∠AOD=60°,CD=2$\sqrt{3}$,则S阴影=( )| A. | $\frac{3\sqrt{3}}{2}$-$\frac{2}{3}$π | B. | $\frac{3\sqrt{3}}{2}$-2π | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{3\sqrt{3}}{2}$-π |
19.下列调查中,最适合采用普查方式的是( )
| A. | 调查一批汽车的使用寿命 | |
| B. | 调查重庆全市市民“五•一”期间计划外出旅游 | |
| C. | 调查某航班的旅客是否携带了违禁物品 | |
| D. | 调查全国初三学生的视力情况 |
16.若点P(a,b)在第一象限,则点P1(-a,-b)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
1.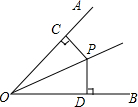 如图,OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C、D,则下列结论错误的是( )
如图,OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C、D,则下列结论错误的是( )
 如图,OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C、D,则下列结论错误的是( )
如图,OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C、D,则下列结论错误的是( )| A. | PC=PD | B. | ∠CPD=∠DOP | C. | ∠CPO=∠DPO | D. | OC=OD |
 如图,二次函数y=x2+bx+c的图象交x轴于A、B两点,交y轴于点C,顶点为点P,经过B、C两点的直线为y=-x+3.
如图,二次函数y=x2+bx+c的图象交x轴于A、B两点,交y轴于点C,顶点为点P,经过B、C两点的直线为y=-x+3.