题目内容
13. 如图,已知矩形ABCD的对角线长为10cm,E、F、G、H分别是AB、BC、CD、DA的中点,则四边形EFGH的周长等于20cm.
如图,已知矩形ABCD的对角线长为10cm,E、F、G、H分别是AB、BC、CD、DA的中点,则四边形EFGH的周长等于20cm.
分析 连接AC、BD,根据三角形的中位线求出HG、GF、EF、EH的长,再求出四边形EFGH的周长即可.
解答 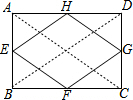 解:如图,连接AC、BD,
解:如图,连接AC、BD,
∵四边形ABCD是矩形,
∴AC=BD=10cm,
∵E、F、G、H分别是AB、BC、CD、DA的中点,
∴HG=EF=$\frac{1}{2}$AC=5cm,EH=FG=$\frac{1}{2}$BD=5cm,
∴四边形EFGH的周长等于5cm+5cm+5cm+5cm=20cm,
故答案为:20.
点评 本题考查了矩形的性质,三角形的中位线的应用,能求出四边形的各个边的长是解此题的关键,注意:矩形的对角线相等,三角形的中位线平行于第三边,并且等于第三边的一半.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.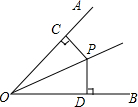 如图,OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C、D,则下列结论错误的是( )
如图,OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C、D,则下列结论错误的是( )
 如图,OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C、D,则下列结论错误的是( )
如图,OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C、D,则下列结论错误的是( )| A. | PC=PD | B. | ∠CPD=∠DOP | C. | ∠CPO=∠DPO | D. | OC=OD |
8.2016年4月6日22:20某市某个观察站测得:空气中pm2.5含量为每立方米23μg,1g=1000000μg,则将23μg用科学记数法表示为( )
| A. | 2.3×107g | B. | 23×10-6g | C. | 2.3×10-5g | D. | 2.3×10-4g |
18.运行程序如图所示,规定:从“输入一个值x”到“结果是否>95”为一次程序操作,如果程序操作进行了三次才停止,那么x的取值范围是( )


| A. | x≥11 | B. | 11≤x<23 | C. | 11<x≤23 | D. | x≤23 |
2.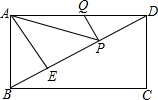 如图,在矩形ABCD中,AD=6,AE⊥BD,垂足为E,ED=3BE,点P、Q分别在BD,AD上,则AP+PQ的最小值为( )
如图,在矩形ABCD中,AD=6,AE⊥BD,垂足为E,ED=3BE,点P、Q分别在BD,AD上,则AP+PQ的最小值为( )
 如图,在矩形ABCD中,AD=6,AE⊥BD,垂足为E,ED=3BE,点P、Q分别在BD,AD上,则AP+PQ的最小值为( )
如图,在矩形ABCD中,AD=6,AE⊥BD,垂足为E,ED=3BE,点P、Q分别在BD,AD上,则AP+PQ的最小值为( )| A. | 2$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{3}$ |
3.下列方程中,没有实数根的是( )
| A. | 2x+3=0 | B. | x2-1=0 | C. | $\frac{2}{x+1}=1$ | D. | x2+x+1=0 |
 如图,在△AOB中,∠AOB为直角,OA=6,OB=8,半径为2的动圆圆心Q从点O出发,沿着OA方向以1个单位长度/秒的速度匀速运动,同时动点P从点A出发,沿着AB方向也以1个单位长度/秒的速度匀速运动,设运动时间为t秒(0<t≤5)以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连结CD、QC.
如图,在△AOB中,∠AOB为直角,OA=6,OB=8,半径为2的动圆圆心Q从点O出发,沿着OA方向以1个单位长度/秒的速度匀速运动,同时动点P从点A出发,沿着AB方向也以1个单位长度/秒的速度匀速运动,设运动时间为t秒(0<t≤5)以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连结CD、QC.