题目内容
11.内角和为540°的多边形是( )| A. |  | B. |  | C. |  | D. |  |
分析 根据多边形的内角和公式(n-2)•180°列式进行计算即可求解.
解答 解:设多边形的边数是n,则
(n-2)•180°=540°,
解得n=5.
故选:C.
点评 本题主要考查了多边形的内角和公式,熟记公式是解题的关键.

练习册系列答案
相关题目
1.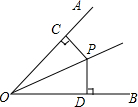 如图,OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C、D,则下列结论错误的是( )
如图,OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C、D,则下列结论错误的是( )
 如图,OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C、D,则下列结论错误的是( )
如图,OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C、D,则下列结论错误的是( )| A. | PC=PD | B. | ∠CPD=∠DOP | C. | ∠CPO=∠DPO | D. | OC=OD |
2.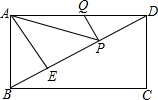 如图,在矩形ABCD中,AD=6,AE⊥BD,垂足为E,ED=3BE,点P、Q分别在BD,AD上,则AP+PQ的最小值为( )
如图,在矩形ABCD中,AD=6,AE⊥BD,垂足为E,ED=3BE,点P、Q分别在BD,AD上,则AP+PQ的最小值为( )
 如图,在矩形ABCD中,AD=6,AE⊥BD,垂足为E,ED=3BE,点P、Q分别在BD,AD上,则AP+PQ的最小值为( )
如图,在矩形ABCD中,AD=6,AE⊥BD,垂足为E,ED=3BE,点P、Q分别在BD,AD上,则AP+PQ的最小值为( )| A. | 2$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{3}$ |
6. 如图是某几何体的三视图,该几何体是( )
如图是某几何体的三视图,该几何体是( )
 如图是某几何体的三视图,该几何体是( )
如图是某几何体的三视图,该几何体是( )| A. | 球 | B. | 三棱柱 | C. | 圆柱 | D. | 圆锥 |
3.下列方程中,没有实数根的是( )
| A. | 2x+3=0 | B. | x2-1=0 | C. | $\frac{2}{x+1}=1$ | D. | x2+x+1=0 |
 如图,在平面直角坐标系网格中,将△ABC进行位似变换得到△A1B1C1.
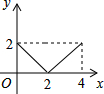
如图,在平面直角坐标系网格中,将△ABC进行位似变换得到△A1B1C1. 如图,正方形ABCD的边长为2cm,动点P从点A出发,在正方形的边上沿A→B→C的方向运动到点C停止,设点P的运动路程为x(cm),在下列图象中,能表示△ADP的面积y(cm2)关于x(cm)的函数关系的图象是( )
如图,正方形ABCD的边长为2cm,动点P从点A出发,在正方形的边上沿A→B→C的方向运动到点C停止,设点P的运动路程为x(cm),在下列图象中,能表示△ADP的面积y(cm2)关于x(cm)的函数关系的图象是( )