题目内容
16.计算:$\sqrt{2}$sin60°-4cos230°-sin45°•tan60°-$\sqrt{(cos60°-tan30°)^{2}}$.分析 原式利用特殊角的三角函数值及二次根式性质计算即可得到结果.
解答 解:原式=$\sqrt{2}$×$\frac{\sqrt{3}}{2}$-4×$\frac{3}{4}$-$\frac{\sqrt{2}}{2}$×$\sqrt{3}$-|$\frac{1}{2}$-$\frac{\sqrt{3}}{3}$|=$\frac{\sqrt{6}}{2}$-3-$\frac{\sqrt{6}}{2}$-$\frac{\sqrt{3}}{3}$+$\frac{1}{2}$=-$\frac{5}{2}$-$\frac{\sqrt{3}}{3}$.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.已知⊙O的内接正六边形周长为36cm,则这个圆的半径是( )
| A. | 3cm | B. | 6cm | C. | 9cm | D. | 12cm |
11.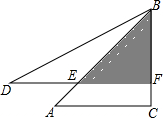 将一副三角板(一个等腰直角三角形和一个锐角为60°的直角三角形)如图所示叠放在一起,若DB=20,则阴影部分的面积为( )
将一副三角板(一个等腰直角三角形和一个锐角为60°的直角三角形)如图所示叠放在一起,若DB=20,则阴影部分的面积为( )
 将一副三角板(一个等腰直角三角形和一个锐角为60°的直角三角形)如图所示叠放在一起,若DB=20,则阴影部分的面积为( )
将一副三角板(一个等腰直角三角形和一个锐角为60°的直角三角形)如图所示叠放在一起,若DB=20,则阴影部分的面积为( )| A. | 50 | B. | 100 | C. | 150 | D. | 200 |
1. 如图,A、O、B在一条直线上,∠1+∠2=90°,∠COD=90°,则图中互补的角有( )
如图,A、O、B在一条直线上,∠1+∠2=90°,∠COD=90°,则图中互补的角有( )
 如图,A、O、B在一条直线上,∠1+∠2=90°,∠COD=90°,则图中互补的角有( )
如图,A、O、B在一条直线上,∠1+∠2=90°,∠COD=90°,则图中互补的角有( )| A. | 3对 | B. | 4对 | C. | 5对 | D. | 6对 |
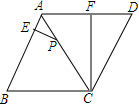 如图,在菱形ABCD中,点P在对角线AC上,且PC=2PA,PE⊥AB于E,CF⊥AD于F,PE=2,求CF的长.
如图,在菱形ABCD中,点P在对角线AC上,且PC=2PA,PE⊥AB于E,CF⊥AD于F,PE=2,求CF的长.