题目内容
7．已知⊙O的内接正六边形周长为36cm，则这个圆的半径是（ ）| A． | 3cm | B． | 6cm | C． | 9cm | D． | 12cm |
分析 首先求出∠BOC=60°，进而证明△OBC为等边三角形，问题即可解决．
解答 解：如图所示，
连接OB、OC，
∵⊙O的内接正六边形ABCDEF的周长为36cm，
∴边长BC=6cm；
∵∠BOC=$\frac{360°}{6}$=60°，且OC=OB，
∴△OBC为等边三角形，
∴OB=BC=6cm，
即该圆的半径为6cm．
故选：B．
点评 本题考查了正六边形的性质、正六边形和圆；熟练掌握正六边形的性质，证明三角形是等边三角形是解决问题的关键．
练习册系列答案
相关题目
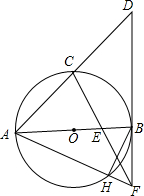如图，AB是⊙O的直径，C是$\widehat{AB}$的中点，连结AC并延长到点D，使AC=CD，E是OB的中点，连结CE并延长交DB于点F．