题目内容
18. 如图,AB为⊙O的直径,BC切⊙O于点B,AC交⊙O于点D,E为BC中点.求证:DE为⊙O的切线.
如图,AB为⊙O的直径,BC切⊙O于点B,AC交⊙O于点D,E为BC中点.求证:DE为⊙O的切线.
分析 先连接OD和BD,根据圆周角定理求出∠ADB=90°,根据直角三角形斜边上中线性质求出DE=BE,推出∠EDB=∠EBD,∠ODB=∠OBD,即可求出∠ODE=90°,根据切线的判定推出即可.
解答  证明:连接OD,BD,
证明:连接OD,BD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠BDC=90°,
∵E为BC的中点,
∴DE=BE=CE,
∴∠EDB=∠EBD,
∵OD=OB,
∴∠ODB=∠OBD,
∵BC切⊙O于点B,
∴∠ABC=90°,
∴∠EDO=∠EDB+∠ODB=∠EBD+∠OBD=∠ABC=90°,
∴OD⊥DE,
∴DE是⊙O的切线.
点评 本题考查了切线的判定和性质,直角三角形的性质,圆周角定理的应用,解此题的关键是求出∠ODE=90°,注意:经过半径的外端,并且垂直于这条半径的直线是圆的切线.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
13.已知一次函数y=kx+2(k≠0)的函数值y随x的增大而增大,点A在此函数图象上,则点A坐标不可能是( )
| A. | (2,3) | B. | (-3,-1) | C. | (3,-1) | D. | (-1,1) |
3. 如图,PA、PB分别切⊙O于点A、B,点E是⊙O上一点,且∠AEB=50°,则∠P=( )
如图,PA、PB分别切⊙O于点A、B,点E是⊙O上一点,且∠AEB=50°,则∠P=( )
 如图,PA、PB分别切⊙O于点A、B,点E是⊙O上一点,且∠AEB=50°,则∠P=( )
如图,PA、PB分别切⊙O于点A、B,点E是⊙O上一点,且∠AEB=50°,则∠P=( )| A. | 100° | B. | 80° | C. | 60° | D. | 50° |
10.甲,乙,丙三地的海拔高度为20米,-15米,-10米,那么最高地方是( )
| A. | 20米 | B. | -10米 | C. | -15米 | D. | 15米 |
7.如果多项式y2-2my+1是完全平方式,那么m的值为( )
| A. | 1 | B. | -1 | C. | ±1 | D. | 无法确定 |
8.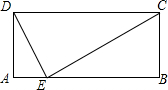 矩形ABCD中,AD=5,DC=12,在AB上找一点E,使点E与点C、点D的连线将此矩形分成三个相似三角形.这样的点存在吗?( )
矩形ABCD中,AD=5,DC=12,在AB上找一点E,使点E与点C、点D的连线将此矩形分成三个相似三角形.这样的点存在吗?( )
 矩形ABCD中,AD=5,DC=12,在AB上找一点E,使点E与点C、点D的连线将此矩形分成三个相似三角形.这样的点存在吗?( )
矩形ABCD中,AD=5,DC=12,在AB上找一点E,使点E与点C、点D的连线将此矩形分成三个相似三角形.这样的点存在吗?( )| A. | 有一个点 | B. | 有两个点 | C. | 不存在 | D. | 无法确定 |
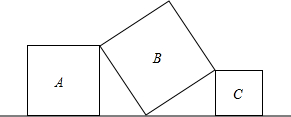 如图,将三个大小不同的正方形如图放置,顶点处两两相接,若正方形A的边长为6,C的边长为4,则正方形B的面积为52.
如图,将三个大小不同的正方形如图放置,顶点处两两相接,若正方形A的边长为6,C的边长为4,则正方形B的面积为52.