题目内容
3.某药业生产厂家为支援灾区人民,准备捐赠一批某种急需药品,该厂家备有多辆甲、乙两种型号的货车,甲型号车每辆牢装满时能装60箱,乙型号车每辆车袋满时能装70箱,如果单独用甲型号车若干辆,则装满每车后还余20箱未装;如果单独用同样辆数的乙型号车装,则装完后还可以再装30箱.(1)求这批药品有多少箱?
(2)已知将这批药品从厂家运到灾区,甲、乙两型号车的运输成本分别为320元/辆和350元/辆,请你提出一个派车方案,保证这批药品装完,且运输总成本最低.并求出这个最低运输成本.
分析 (1)设这批药品有x箱,分别表示出需要甲、乙车辆的辆数,利用辆数相等列出方程解答即可;
(2)设需要甲型号车u辆,乙型号车v辆,总费用为z,列出z的解析式,从极端考虑探讨得出答案即可.
解答 解:(1)设这批药品有x箱,由题意得
$\frac{x-20}{60}$=$\frac{x+30}{70}$,
解得:x=320;
(2)设需要甲型号车u辆,乙型号车v辆,总费用为z,由题意得
z=320u+350v,60u+70v≥320.
派车预设方案如下:
| 甲车u(辆) | 甲车u辆成本 | 乙车v(辆) | 乙车v辆成本 | 总成本z(元) |
| 6 | 1920 | 0 | 0 | 1920 |
| 5 | 1600 | 1 | 350 | 1950 |
| 4 | 1280 | 2 | 700 | 1980 |
| 3 | 960 | 2 | 700 | 1660 |
| 2 | 640 | 3 | 1050 | 1690 |
| 1 | 320 | 4 | 1400 | 1720 |
| 0 | 0 | 5 | 1750 | 1750 |
且z=1660(元).
所以这个最低运输成本为1660元.
点评 此题考查一元一次方程的实际运用,一次函数的实际运用,利用列举的方法,从极端考虑解决问题.

练习册系列答案
相关题目
13.已知一次函数y=kx+2(k≠0)的函数值y随x的增大而增大,点A在此函数图象上,则点A坐标不可能是( )
| A. | (2,3) | B. | (-3,-1) | C. | (3,-1) | D. | (-1,1) |
14. 如图,PA,PB分别与⊙O相切于A,B两点,∠P=70°,则∠C为( )
如图,PA,PB分别与⊙O相切于A,B两点,∠P=70°,则∠C为( )
 如图,PA,PB分别与⊙O相切于A,B两点,∠P=70°,则∠C为( )
如图,PA,PB分别与⊙O相切于A,B两点,∠P=70°,则∠C为( )| A. | 55° | B. | 70° | C. | 110° | D. | 140° |
11. 如图中,到原点距离相等的两个点是( )
如图中,到原点距离相等的两个点是( )
 如图中,到原点距离相等的两个点是( )
如图中,到原点距离相等的两个点是( )| A. | 点M与点Q | B. | 点N与点P | C. | 点M与点P | D. | 点N与点Q |
18. 要测量河两岸相对的两点A、B的距离,先在AB的垂线上取两点C、D,使 BC=CD,再作出BF的垂线DE,使E与A、C在一条直线上(如图所示),可以测得DE的长就是AB的长(即测得河宽),可由△EDC≌△ABC得到,判定这两个三角形全等的理由是( )
要测量河两岸相对的两点A、B的距离,先在AB的垂线上取两点C、D,使 BC=CD,再作出BF的垂线DE,使E与A、C在一条直线上(如图所示),可以测得DE的长就是AB的长(即测得河宽),可由△EDC≌△ABC得到,判定这两个三角形全等的理由是( )
 要测量河两岸相对的两点A、B的距离,先在AB的垂线上取两点C、D,使 BC=CD,再作出BF的垂线DE,使E与A、C在一条直线上(如图所示),可以测得DE的长就是AB的长(即测得河宽),可由△EDC≌△ABC得到,判定这两个三角形全等的理由是( )
要测量河两岸相对的两点A、B的距离,先在AB的垂线上取两点C、D,使 BC=CD,再作出BF的垂线DE,使E与A、C在一条直线上(如图所示),可以测得DE的长就是AB的长(即测得河宽),可由△EDC≌△ABC得到,判定这两个三角形全等的理由是( )| A. | 边角边 | B. | 角边角 | C. | 边边边 | D. | 边边角 |
8.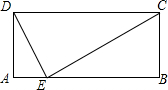 矩形ABCD中,AD=5,DC=12,在AB上找一点E,使点E与点C、点D的连线将此矩形分成三个相似三角形.这样的点存在吗?( )
矩形ABCD中,AD=5,DC=12,在AB上找一点E,使点E与点C、点D的连线将此矩形分成三个相似三角形.这样的点存在吗?( )
 矩形ABCD中,AD=5,DC=12,在AB上找一点E,使点E与点C、点D的连线将此矩形分成三个相似三角形.这样的点存在吗?( )
矩形ABCD中,AD=5,DC=12,在AB上找一点E,使点E与点C、点D的连线将此矩形分成三个相似三角形.这样的点存在吗?( )| A. | 有一个点 | B. | 有两个点 | C. | 不存在 | D. | 无法确定 |
12.一组数据a、b、c、d、e、f、g的平均数是m,方差是n,则另一组数据2a-3、2b-3、2c-3、2d-3、2e-3、2f-3、2g-3的平均数和方差分别是( )
| A. | 2m、2n-3 | B. | 2m-3、n | C. | m-3、2n | D. | 2m-3、4n |
13.下列事件中,属于必然事件的是( )
| A. | 打开电视,它正在播广告 | |
| B. | 掷两枚质地均匀的骰子,点数之和一定大于6 | |
| C. | 某射击运动员射击一次,命中靶心 | |
| D. | 早晨的太阳从东方升起 |
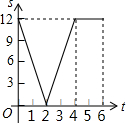
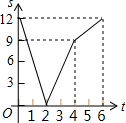
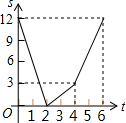
 如图,己知线段AB=12厘米,动点P以2厘米/秒的速度从点A出发向点B运动,动点Q以4厘米/秒的速度从点B出发向点A运动.两点同时出发,到达各自的终点后停止运动.设两点之间的距离为s(厘米),动点P的运动时间为t秒,则下图中能正确反映s与t之间的函数关系的是( )
如图,己知线段AB=12厘米,动点P以2厘米/秒的速度从点A出发向点B运动,动点Q以4厘米/秒的速度从点B出发向点A运动.两点同时出发,到达各自的终点后停止运动.设两点之间的距离为s(厘米),动点P的运动时间为t秒,则下图中能正确反映s与t之间的函数关系的是( )