题目内容
5.若|a|=5,|b|=2,|c|=6且|a+b|=-(a+b),|a+c|=a+c,求a-b+c的值.分析 由|a|=5,|b|=2,|c|=6,得出a=±5,b=±2,c=±6.又因|a+b|=-(a+b),|a+c|=a+c,可得a=-5,b=±2,c=6.从而有两种情况:①当a=-5,b=2,c=6时,a-b+c=-5-2+6=-1;②a=-5,b=-2,c=6时,a-b+c=-5+2+6=3.
解答 解:∵|a|=5,|b|=2,|c|=6,
∴a=±5,b=±2,c=±6,
∵|a+b|=-(a+b),|a+c|=a+c,
∴a=-5,b=±2,c=6,
有两种情况:①当a=-5,b=2,c=6时,a-b+c=-5-2+6=-1;
②a=-5,b=-2,c=6时,a-b+c=-5+2+6=3.
点评 本题主要考查了绝对值的性质,一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0,灵活运用该规律是解答此题的关键.

练习册系列答案
相关题目

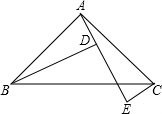 已知在△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,BD⊥AE于点D,CE⊥AE于点E.
已知在△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,BD⊥AE于点D,CE⊥AE于点E. 某学校为了了解800名初中毕业生体育考试成绩的情况(满分30分,得分为整数),从中随机抽取了部分学生的体育考试成绩,制成如下图所示的频数分布直方图.已知成绩在18.5~21.5这一组的频率为0.12,请回答下列问题:
某学校为了了解800名初中毕业生体育考试成绩的情况(满分30分,得分为整数),从中随机抽取了部分学生的体育考试成绩,制成如下图所示的频数分布直方图.已知成绩在18.5~21.5这一组的频率为0.12,请回答下列问题: