题目内容
14.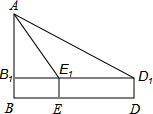 在一次课外实践活动中,老师要求同学们利用测角仪和皮尺估测教学楼AB的高度.同学们在教学楼的正前方D处用高为1米的测角仪测的教学楼顶端A的仰角为30°,然后他们向教学楼方向前进30米到达E处,又测得A的仰角为60°,则教学楼高度AB是多少米?(精确到0.1米,参考数据$\sqrt{3}$=1.732)
在一次课外实践活动中,老师要求同学们利用测角仪和皮尺估测教学楼AB的高度.同学们在教学楼的正前方D处用高为1米的测角仪测的教学楼顶端A的仰角为30°,然后他们向教学楼方向前进30米到达E处,又测得A的仰角为60°,则教学楼高度AB是多少米?(精确到0.1米,参考数据$\sqrt{3}$=1.732)
分析 设AB1=x米,根据正切的概念用x分别表示出B1E1、B1D1,根据题意列出方程,解方程即可.
解答 解:设AB1=x米,
由题意得,∠AD1B1=30°,∠AE1B1=60°,
∴B1E1=$\frac{A{B}_{1}}{tan∠A{E}_{1}{B}_{1}}$=$\frac{\sqrt{3}}{3}$x,
B1D1=$\frac{{A}_{1}{B}_{1}}{tan∠A{D}_{1}{B}_{1}}$=$\sqrt{3}$x,
则$\sqrt{3}$x-$\frac{\sqrt{3}}{3}$x=30,
解得,x=15$\sqrt{3}$,
则AB=15$\sqrt{3}$+1≈27.0米,
答:教学楼高度AB约为27.0米.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,解决此类问题要了解角之间的关系,找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作高或垂线构造直角三角形,另当问题以一个实际问题的形式给出时,要善于读懂题意,把实际问题划归为直角三角形中边角关系问题加以解决.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
2.在下列调查中,适宜采用普查方式的是( )
| A. | 了解全国中学生的视力情况 | |
| B. | 了解九(1)班学生鞋子的尺码情况 | |
| C. | 检测一批电灯泡的使用寿命 | |
| D. | 调查郑州电视台《郑州大民生》栏目的收视率 |
19.在平面直角坐标系中,如果抛物线y=3x2不动,而把x轴、y轴分别向上、向右平移2个单位,那么在新坐标系中抛物线的解析式是( )
| A. | y=3(x-2)2+2 | B. | y=3(x+2)2-2 | C. | y=3(x-2)2+2 | D. | y=3(x+2)2+2 |
4.我市飞鹤中学初三(一)班某小组7位学生的中考体育测试成绩(满分30分)依次为27,30,29,27,30,28,30.则这组数据的众数与中位数分别是( )
| A. | 30,27 | B. | 30,29 | C. | 29,30 | D. | 30,28 |
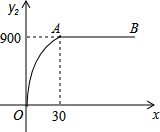 成都地铁规划到2020年将通车13条线路,近几年正是成都地铁加紧建设和密集开通的几年,市场对建材的需求量有所提高,根据市场调查分析可预测:投资水泥生产销售后所获得的利润y1(万元)与投资资金量x(万元)满足正比例关系y1=20x;投资钢材生产销售的后所获得的利润y2(万元)与投资资金量x(万元)满足函数关系的图象如图所示(其中OA是抛物线的一部分,A为抛物线的顶点,AB∥x轴).
成都地铁规划到2020年将通车13条线路,近几年正是成都地铁加紧建设和密集开通的几年,市场对建材的需求量有所提高,根据市场调查分析可预测:投资水泥生产销售后所获得的利润y1(万元)与投资资金量x(万元)满足正比例关系y1=20x;投资钢材生产销售的后所获得的利润y2(万元)与投资资金量x(万元)满足函数关系的图象如图所示(其中OA是抛物线的一部分,A为抛物线的顶点,AB∥x轴).

 如图,为了开发利用海洋资源,我勘测飞机测量钓鱼岛附属岛屿之一的北小岛(又称为鸟岛)两侧端点A,B的距离,飞机在距海平面垂直高度为100米的北小岛上方点C处测得端点A的俯角为30°,测得端点B的俯角为45°,求北小岛两侧端点A,B的距离(结果精确到1米,$\sqrt{3}$≈1.732)
如图,为了开发利用海洋资源,我勘测飞机测量钓鱼岛附属岛屿之一的北小岛(又称为鸟岛)两侧端点A,B的距离,飞机在距海平面垂直高度为100米的北小岛上方点C处测得端点A的俯角为30°,测得端点B的俯角为45°,求北小岛两侧端点A,B的距离(结果精确到1米,$\sqrt{3}$≈1.732)