题目内容
在三角形ABC中,BC=a,AC=b,AB=c,且满足
=
=k
①求证:k=
;
②求证:c>b;
③当k=2时,证明:ab是△ABC最大边.
| a+3 |
| c-b |
| a(a-1) |
| c-b |
①求证:k=
| a2+3 |
| 2c |
②求证:c>b;
③当k=2时,证明:ab是△ABC最大边.
考点:三角形边角关系
专题:
分析:(1)运用比例的有关性质将所给的代数式,恒等变形,即可解决问题.
(2)根据k>0,结合c与k的关系,比较分析即可解决问题.
(3)根据题意,用a分别表示出b、c的值,灵活运用一元二次不等式的有关知识进行比较、分析、探究,即可解决问题.
(2)根据k>0,结合c与k的关系,比较分析即可解决问题.
(3)根据题意,用a分别表示出b、c的值,灵活运用一元二次不等式的有关知识进行比较、分析、探究,即可解决问题.
解答:解析:(1)∵
=
=k,
∴
=
,
∴
=
,
∴
=
,
∴k=
.
(2)∵k=
>0,而
=k,a+3>0,
∴c-b>0,c>b.
(3)当k=2时,
∵
=
=2,
∴
,
由①+②并解得:c=
;
由②-①并解得:b=
;
∵b>0,即
>0,
解得:a>3或 a<-1(舍去);
∵c-a=
=
,且a>3,
∴c-a>0,c>a;由(2)知c>b,
∴AB是的△ABC最大边.
| a+3 |
| c-b |
| a(a-1) |
| c+b |
∴
| c+b |
| c-b |
| a2-a |
| a+3 |
∴
| 2c |
| c-b |
| a2+3 |
| a+3 |
∴
| a+3 |
| c-b |
| a2+3 |
| 2c |
∴k=
| a2+3 |
| 2c |
(2)∵k=
| a2+3 |
| 2c |
| a+3 |
| c-b |
∴c-b>0,c>b.
(3)当k=2时,
∵
| a+3 |
| c-b |
| a2-a |
| b+c |
∴
|
由①+②并解得:c=
| a2+3 |
| 4 |
由②-①并解得:b=
| a2-2a-3 |
| 4 |
∵b>0,即
| a2-2a-3 |
| 4 |
解得:a>3或 a<-1(舍去);
∵c-a=
| a2-4a+3 |
| 4 |
| (a-3)(a-1) |
| 4 |
∴c-a>0,c>a;由(2)知c>b,
∴AB是的△ABC最大边.
点评:本题主要考查了三角形的三边关系及其应用问题;同时还渗透了对一元二次不等式等重要代数知识的考查;解题的关键是深入分析式子的结构特点,大胆猜测推理,科学求解论证;对求解变形能力、综合运用能力等均提出了较高的要求.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
 如图放置的是一副斜边相等的直角三角板,连接BD交公共的斜边AC于O.
如图放置的是一副斜边相等的直角三角板,连接BD交公共的斜边AC于O.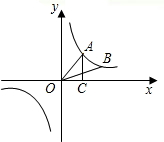 如图,点A、B在反比例函数
如图,点A、B在反比例函数 如图是三角形ABC,三边可表示成线段AB,线段AC,线段BC,则在下面横线上填入“>”“<“或“=”,并说明理由.
如图是三角形ABC,三边可表示成线段AB,线段AC,线段BC,则在下面横线上填入“>”“<“或“=”,并说明理由.