题目内容
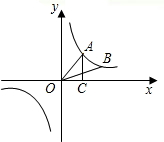 如图,点A、B在反比例函数y=
如图,点A、B在反比例函数y=| k |
| x |
(1)该反比例函数的解析式;
(2)△AOC的面积.
考点:待定系数法求反比例函数解析式,反比例函数系数k的几何意义
专题:计算题
分析:(1)把A横坐标代入反比例解析式表示出纵坐标,即为AC的长,求出B到AC边的高,根据题中三角形ABC面积为2求出k的值,即可确定出解析式;
(2)由A坐标得到AC与OC的长,求出三角形AOC面积即可.
(2)由A坐标得到AC与OC的长,求出三角形AOC面积即可.
解答:解:(1)由题意得:A(a,
),即AC=
,
∵S△ABC=
AC•h=
•
•(2a-a)=2,
解得:k=4,
则反比例解析式为y=
;
(2)由A(a,
),得到OC=a,AC=
,
则S△AOC=
AC•OC=
a•
=2.
| k |
| a |
| k |
| a |
∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| k |
| a |
解得:k=4,
则反比例解析式为y=
| 4 |
| x |
(2)由A(a,
| 4 |
| a |
| 4 |
| a |
则S△AOC=
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| a |
点评:此题考查了待定系数法求反比例解析式,以及反比例函数系数k的几何意义,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
若2x-y-2013=0,则2y-4x+2014的值为( )
| A、2012 | B、-2012 |
| C、1 | D、-1 |
 画出下面物体的正投影(正三棱柱)
画出下面物体的正投影(正三棱柱)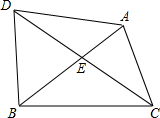 四边形ADBC中,∠ADB=∠ACB,CD平分∠ACB交AB于点E,且BE=CE.若BC=6,AC=4,则BD=
四边形ADBC中,∠ADB=∠ACB,CD平分∠ACB交AB于点E,且BE=CE.若BC=6,AC=4,则BD=