题目内容
8.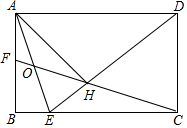 如图,在矩形ABCD中,BC=$\sqrt{2}$AB,∠ADC的平分线交边BC于点E,AH⊥DE于点H,连接CH并延长交边AB于点F,连接AE交CF于点O,给出下列命题:
如图,在矩形ABCD中,BC=$\sqrt{2}$AB,∠ADC的平分线交边BC于点E,AH⊥DE于点H,连接CH并延长交边AB于点F,连接AE交CF于点O,给出下列命题:(1)∠AEB=∠AEH (2)DH=2$\sqrt{2}$EH
(3)OH=$\frac{1}{2}$AE (4)BC-BF=$\sqrt{2}$EH
其中正确命题的序号( )
| A. | (1)(2)(3) | B. | (2)(3)(4) | C. | (2)(4) | D. | (1)(3) |
分析 (1)根据矩形的性质得到AD=BC=$\sqrt{2}$AB=$\sqrt{2}$CD,由DE平分∠ADC,得到△ADH是等腰直角三角形,△DEC是等腰直角三角形,得到DE=$\sqrt{2}$CD,得到等腰三角形求出∠AED=67.5°,∠AEB=67.5°,得到(1)正确;
(2)设DH=1,则AH=DH=1,AD=DE=$\sqrt{2}$,求出HE=$\sqrt{2}$-1,得到2$\sqrt{2}$HE≠1,所以(2)不正确;
(3)通过角的度数求出△AOH和△OEH是等腰三角形,从而得到(3)正确;
(4)由△AFH≌△CHE,到AF=EH,由△ABE≌△AHE,得到BE=EH,于是得到BC-BF=(BE+CE)-(AB-AF)=(CD+EH)-(CD-EH)=2EH,从而得到(4)不正确.
解答 解:(1)在矩形ABCD中,AD=BC=$\sqrt{2}$AB=$\sqrt{2}$CD,∠ADC=∠BCD=90°,
∵DE平分∠ADC,
∴∠ADE=∠CDE=45°,
∵AH⊥DE,
∴△ADH是等腰直角三角形,
∴AD=$\sqrt{2}$AH,
∴AH=AB=CD,
∵△DEC是等腰直角三角形,
∴DE=$\sqrt{2}$CD,
∴AD=DE,
∴∠AED=67.5°,
∴∠AEB=180°-45°-67.5°=67.5°,
∴∠AEH=∠AEB,
所以(1)结论正确;
(2)设DH=1,
则AH=DH=1,AD=DE=$\sqrt{2}$,
∴HE=DE-DH=$\sqrt{2}$-1,
∴2$\sqrt{2}$HE=2$\sqrt{2}$($\sqrt{2}$-1)=4-2$\sqrt{2}$≠1,
所以(2)结论不正确;
(3)∵∠AEH=67.5°,
∴∠EAH=22.5°,
∵DH=CD,∠EDC=45°,
∴∠DHC=67.5°,
∴∠OHA=180°-90°-67.5°=22.5°,
∴∠OAH=∠OHA=22.5°,
∴OA=OH,
∴∠AEH=∠OHE=67.5°,
∴OH=OE=OA,
∴OH=$\frac{1}{2}$AE,
所以(3)正确;
(4)∵AH=DH,CD=CE,
在△AFH与△CHE中,
$\left\{\begin{array}{l}{∠AHF=∠HCE=22.5°}\\{∠FAH=∠HEC=45°}\\{AH=CE}\end{array}\right.$,
∴△AFH≌△CHE,
∴AF=EH,
在Rt△ABE与Rt△AHE中,
$\left\{\begin{array}{l}{∠B=∠AHE=90°}\\{∠BEA=∠HEA}\\{AE=AE}\end{array}\right.$,
∴△ABE≌△AHE,
∴BE=EH,
∴BC-BF=(BE+CE)-(AB-AF)=(CD+EH)-(CD-EH)=2EH,
所以(2)不正确,
故选D.
点评 本题考查了矩形的性质,全等三角形的判定与性质,角平分线的定义,等腰三角形的判定与性质,熟记各性质并仔细分析题目条件,根据相等的度数求出相等的角,从而得到三角形全等的条件或判断出等腰三角形是解题的关键,也是本题的难点.

| A. | sin20°<sin40°<sin70° | B. | cos20°<cos40°<cos70° | ||
| C. | tan20°<tan40°<tan70° | D. | sin30°<cos45°<tan60° |
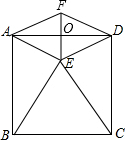 如图,正方形ABCD的边长为2,以BC为边向正方形内作等边△BCE,连接AE、DE.
如图,正方形ABCD的边长为2,以BC为边向正方形内作等边△BCE,连接AE、DE.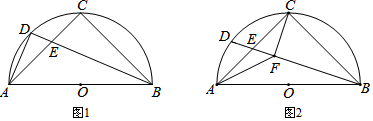
 如图,作出△ABC的三条高.
如图,作出△ABC的三条高.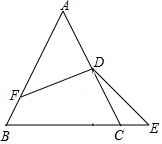 已知△ABC是等边三角形,D是AC的中点,F为AB边上一点,且AF=2BF,E为射线BC上一点,∠EDF=120°,则$\frac{CE}{CD}$=$\frac{1}{3}$.
已知△ABC是等边三角形,D是AC的中点,F为AB边上一点,且AF=2BF,E为射线BC上一点,∠EDF=120°,则$\frac{CE}{CD}$=$\frac{1}{3}$. 如图,在等腰三角形ABC中,AB=AC,以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系,抛物线y=0.5x2-3.5x-4经过A、B两点.若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移,分别交线段OA、CA和抛物线于点E、M和点P,连结PA、PB.设直线l移动的时间为t(0<t<4)秒,求四边形PBCA的面积S(面积单位)与t(秒)的函数关系式,并求出四边形PBCA的最大面积.
如图,在等腰三角形ABC中,AB=AC,以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系,抛物线y=0.5x2-3.5x-4经过A、B两点.若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移,分别交线段OA、CA和抛物线于点E、M和点P,连结PA、PB.设直线l移动的时间为t(0<t<4)秒,求四边形PBCA的面积S(面积单位)与t(秒)的函数关系式,并求出四边形PBCA的最大面积.