题目内容
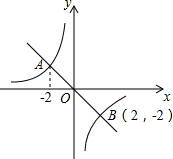 如图,在平面直角坐标系xOy中,一次函数y1=kx的图象与反比例函数y2=
如图,在平面直角坐标系xOy中,一次函数y1=kx的图象与反比例函数y2=| m |
| x |
(1)根据图象,求一次函数和反比例函数解析式;
(2)根据图象直接写出kx>
| m |
| x |
(3)若点P在y轴上,且满足以点A、B、P为顶点的三角形是直角三角形,试直接写出点P所有可能的坐标为
考点:反比例函数与一次函数的交点问题
专题:计算题
分析:(1)直接把B点坐标分别代入y1=kx和y2=
中,求出khe1m的值,从而得到一次函数和反比例函数解析式;
(2)观察函数图象得到当x<-2或0<x<2时,一次函数图象都在反比例函数图象的上方,即有kx>
;
(3)设P点坐标为(0,t),而A(-2,2),B(2,-2),根据两点间的距离公式实数PA2=22+(t-2)2,PB2=22+(t+2)2,AB2=42+42=32,然后分类讨论:当∠APB=90°时,根据勾股定理得22+(t-2)2+22+(t+2)2=32;当∠PAB=90°时,根据勾股定理得22+(t-2)2+32=22+(t+2)2;
当∠PBA=90°时,根据勾股定理得22+(t+2)2+32=22+(t-2)2,再分别解方程求出t的值,最后写出P点坐标.
| m |
| x |
(2)观察函数图象得到当x<-2或0<x<2时,一次函数图象都在反比例函数图象的上方,即有kx>
| m |
| x |
(3)设P点坐标为(0,t),而A(-2,2),B(2,-2),根据两点间的距离公式实数PA2=22+(t-2)2,PB2=22+(t+2)2,AB2=42+42=32,然后分类讨论:当∠APB=90°时,根据勾股定理得22+(t-2)2+22+(t+2)2=32;当∠PAB=90°时,根据勾股定理得22+(t-2)2+32=22+(t+2)2;
当∠PBA=90°时,根据勾股定理得22+(t+2)2+32=22+(t-2)2,再分别解方程求出t的值,最后写出P点坐标.
解答:解:(1)把B(2,-2)代入y1=kx得k=-1,
∴一次函数解析式为y1=-x;
把B(2,-2)代入y2=
得m=2×(-2)=-4,
∴反比例函数解析式为y2=-
;
(2)把x=-2代入y2=-
得y=2,
∴A点坐标为(-2,2),
∴当x<-2或0<x<2时,kx>
;
(3)设P点坐标为(0,t),而A(-2,2),B(2,-2),
∴PA2=22+(t-2)2,PB2=22+(t+2)2,AB2=42+42=32,
当∠APB=90°时,则PA2+PB2=AB2,即22+(t-2)2+22+(t+2)2=32,解得t=±2
,此时P点坐标为(0,2
)或(0,-2
);
当∠PAB=90°时,则PA2+AB2=PB2,即22+(t-2)2+32=22+(t+2)2,解得t=4,此时P点坐标为(0,4);
当∠PBA=90°时,则PB2+AB2=PA2,即22+(t+2)2+32=22+(t-2)2,解得t=-4,此时P点坐标为(0,-4);
综上所述,P点坐标为(0,4)、(0,-4)、(0,2
)、(0,-2
).
故答案为x<-2或0<x<2;(0,4)、(0,-4)、(0,2
)、(0,-2
).
∴一次函数解析式为y1=-x;
把B(2,-2)代入y2=
| m |
| x |
∴反比例函数解析式为y2=-
| 4 |
| x |
(2)把x=-2代入y2=-
| 4 |
| x |
∴A点坐标为(-2,2),
∴当x<-2或0<x<2时,kx>
| m |
| x |
(3)设P点坐标为(0,t),而A(-2,2),B(2,-2),
∴PA2=22+(t-2)2,PB2=22+(t+2)2,AB2=42+42=32,
当∠APB=90°时,则PA2+PB2=AB2,即22+(t-2)2+22+(t+2)2=32,解得t=±2
| 2 |
| 2 |
| 2 |
当∠PAB=90°时,则PA2+AB2=PB2,即22+(t-2)2+32=22+(t+2)2,解得t=4,此时P点坐标为(0,4);
当∠PBA=90°时,则PB2+AB2=PA2,即22+(t+2)2+32=22+(t-2)2,解得t=-4,此时P点坐标为(0,-4);
综上所述,P点坐标为(0,4)、(0,-4)、(0,2
| 2 |
| 2 |
故答案为x<-2或0<x<2;(0,4)、(0,-4)、(0,2
| 2 |
| 2 |
点评:本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.也考查了勾股定理基恩分类讨论的思想.

练习册系列答案
相关题目
化简
的结果是( )
| 40 |
| A、20 | ||
B、2
| ||
C、2
| ||
D、4
|
由2x+y=1得到用x的代数式表示y的式子为( )
| A、y=1-2x | ||
| B、y=1+2x | ||
C、x=
| ||
D、x=
|




 如图,点A(2,6)和点B(点B在点A的右侧)在反比例函数的图象上,点C在y轴上,BC∥x轴,tan∠ACB=2,二次函数的图象经过A、B、C三点.
如图,点A(2,6)和点B(点B在点A的右侧)在反比例函数的图象上,点C在y轴上,BC∥x轴,tan∠ACB=2,二次函数的图象经过A、B、C三点.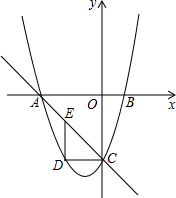 已知抛物线与x轴交于A(-3,0)、B(1,0)两点,交y轴于点C(0,-3),点E为直线AC上的一动点,DE∥y轴交抛物线于点D.
已知抛物线与x轴交于A(-3,0)、B(1,0)两点,交y轴于点C(0,-3),点E为直线AC上的一动点,DE∥y轴交抛物线于点D.