题目内容
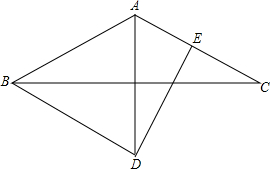 如图,△ABC是等腰三角形,AB=AC,∠CBD=30°,DE垂直平分AC,求证:AB=AD.
如图,△ABC是等腰三角形,AB=AC,∠CBD=30°,DE垂直平分AC,求证:AB=AD.考点:全等三角形的判定与性质
专题:证明题
分析:过点A作AF⊥BC于F,过点C作CG⊥BD交BD的延长线于G,连接CD、EF、EG、FG,根据等腰三角形三线合一的性质可得BF=CF=
BC,根据直角三角形斜边上的中线等于斜边的一半可得FG=
BC,根据直角三角形两锐角互余求出∠BCG=60°,然后判断出△CFG是等边三角形,根据等边三角形的性质可得FG=CG,根据直角三角形斜边上的中线等于斜边的一半可得EF=CE=
AC,再利用“边边边”证明△ECG和△EFG全等,根据全等三角形对应角相等可得∠EGC=∠EGF=30°,再求出点E、F、G、C四点共圆,根据同弧所对的圆周角相等求出∠CDE=∠EGC=30°,然后求出∠ACD=60°,根据线段垂直平分线上的点到两端点的距离相等可得AD=CD,然后判断出△ACD是等边三角形,根据等边三角形的性质可得AD=AC,然后等量代换即可得证.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:证明:如图,过点A作AF⊥BC于F,过点C作CG⊥BD交BD的延长线于G,连接CD、EF、EG、FG,
∵AB=AC,
∴BF=CF=
BC,
∴FG=CF=
BC,
∵∠CBD=30°,
∴∠BCG=90°-30°=60°,
∴△CFG是等边三角形,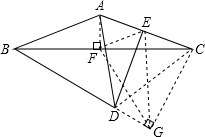
∴FG=CG,∠CGF=60°,
∵DE垂直平分AC,
∴点E是AC的中点,
∴EF=CE=
AC,
在△ECG和△EFG中,
,
∴△ECG≌△EFG(SSS),
∴∠EGC=∠EGF=
∠CGF=
×60°=30°,
∵∠BGC=∠CED=90°,
∴点E、D、G、C四点共圆,
∴∠CDE=∠EGC=30°,
∴∠ACD=90°-∠CDE=90°-30°=60°,
∵DE垂直平分AC,
∴AD=CD,
∴△ACD是等边三角形,
∴AD=AC,
∵AB=AC,
∴AB=AD.
∵AB=AC,
∴BF=CF=
| 1 |
| 2 |
∴FG=CF=
| 1 |
| 2 |
∵∠CBD=30°,
∴∠BCG=90°-30°=60°,
∴△CFG是等边三角形,

∴FG=CG,∠CGF=60°,
∵DE垂直平分AC,
∴点E是AC的中点,
∴EF=CE=
| 1 |
| 2 |
在△ECG和△EFG中,
|
∴△ECG≌△EFG(SSS),
∴∠EGC=∠EGF=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠BGC=∠CED=90°,
∴点E、D、G、C四点共圆,
∴∠CDE=∠EGC=30°,
∴∠ACD=90°-∠CDE=90°-30°=60°,
∵DE垂直平分AC,
∴AD=CD,
∴△ACD是等边三角形,
∴AD=AC,
∵AB=AC,
∴AB=AD.
点评:本题考查了全等三角形的判定与性质,等边三角形的判定与性质,直角三角形斜边上的中线等于斜边的一半的性质,直角三角形两锐角互余的性质,难点在于作辅助线构造出等边三角形和全等三角形,利用四点共圆求出∠CDE=30°是解题的关键.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
 如图所示,过正方形ABCD的顶点A作对角线BD的平行线,在这条直线上取一点E,使BD=ED,且DE与AB交于点F,证明:BE=BF.
如图所示,过正方形ABCD的顶点A作对角线BD的平行线,在这条直线上取一点E,使BD=ED,且DE与AB交于点F,证明:BE=BF.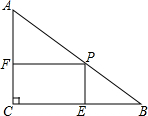 如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=12cm,点P是AB边上的一个动点,过点P作PE⊥BC于点E,PF⊥AC于点F,当PB=
如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=12cm,点P是AB边上的一个动点,过点P作PE⊥BC于点E,PF⊥AC于点F,当PB= 如图,在△ABC中,已知AB=AC,D是BC边上的中点,∠B=30°,则∠DAC=
如图,在△ABC中,已知AB=AC,D是BC边上的中点,∠B=30°,则∠DAC=