题目内容
直线l1:y=3x+n与直线l2:y=kx相交于点B(-2,1).
(1)n= ,k= ,直线y=3x+n与y轴交点的坐标为 ;
(2)若平行于y轴的直线x=t分别交直线l1和l2于点C、D(点C位于点D的上方),是否存在t,使得在y轴上存在点P,以点P、C、D为顶点的三角形是等腰直角三角形?若存在,请求出t的值及相应的点P的坐标;若不存在,请说明理由.
(1)n=
(2)若平行于y轴的直线x=t分别交直线l1和l2于点C、D(点C位于点D的上方),是否存在t,使得在y轴上存在点P,以点P、C、D为顶点的三角形是等腰直角三角形?若存在,请求出t的值及相应的点P的坐标;若不存在,请说明理由.
考点:两条直线相交或平行问题,等腰直角三角形
专题:
分析:(1)可用待定系数法求得n、k的值,从而求得直线L1 的解析式,根据解析式即可求得与y轴的交点坐标;
(2)求得两直线的交点坐标,根据题意t>-2,然后分两种情况分别列出关于t的方程,解方程求得t的值,观察是否合题意,即可判断是否存在t,使得在y轴上存在点P,以点P、C、D为顶点的三角形是等腰直角三角形.
(2)求得两直线的交点坐标,根据题意t>-2,然后分两种情况分别列出关于t的方程,解方程求得t的值,观察是否合题意,即可判断是否存在t,使得在y轴上存在点P,以点P、C、D为顶点的三角形是等腰直角三角形.
解答:解:(1)把B(-2,1)分别代入y=3x+n与y=kx,得
解得:n=7,k=-
,
∴直线l1:y=3x+7;直线l2:y=-
x;
∴直线l1:y=3x+7与y轴交点的坐标为:(0,7).
(2)解
得
,
∵平行于y轴的直线x=t分别交直线l1和l2于点C、D(点C位于点D的上方),
∴t>-2,
设C(t,3t+7),D(t,-
t),
当C、D为直角顶点时,则3t+7+
t=t,解得t=-
<-2(不合题意)
当P为直角顶点时,z则
=t,解得t=-
<-2(不合题意),
所以不存在t,使得在y轴上存在点P,以点P、C、D为顶点的三角形是等腰直角三角形.
|
解得:n=7,k=-
| 1 |
| 2 |
∴直线l1:y=3x+7;直线l2:y=-
| 1 |
| 2 |
∴直线l1:y=3x+7与y轴交点的坐标为:(0,7).
(2)解
|
|
∵平行于y轴的直线x=t分别交直线l1和l2于点C、D(点C位于点D的上方),
∴t>-2,
设C(t,3t+7),D(t,-
| 1 |
| 2 |
当C、D为直角顶点时,则3t+7+
| 1 |
| 2 |
| 14 |
| 5 |
当P为直角顶点时,z则
3t+7+
| ||
| 2 |
| 14 |
| 3 |
所以不存在t,使得在y轴上存在点P,以点P、C、D为顶点的三角形是等腰直角三角形.
点评:此题主要考查了一次函数的综合应用以及等腰直角三角形的性质,根据数形结合进行分类讨论是解题关键,注意不要漏解.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
 同心圆⊙O中,小⊙O和⊙O的半径分别是2
同心圆⊙O中,小⊙O和⊙O的半径分别是2| 10 |
| 5 |
A、15
| ||
B、4
| ||
C、5
| ||
D、8
|
 如图,?ABCD的对角线的交点为点O,点E为CD中点,若S?ABCD=24cm2,求S△AOE的值.
如图,?ABCD的对角线的交点为点O,点E为CD中点,若S?ABCD=24cm2,求S△AOE的值.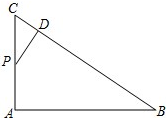 如图,在Rt△ABC中,∠A=90°,P是AC中点,PD⊥BC,D为垂足,BC=9,CD=3.求AB2的值.
如图,在Rt△ABC中,∠A=90°,P是AC中点,PD⊥BC,D为垂足,BC=9,CD=3.求AB2的值. 观察下图,图中有多少同位角、内错角、同旁内角?请把它们列出来.
观察下图,图中有多少同位角、内错角、同旁内角?请把它们列出来.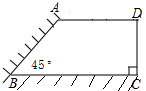 校园要建苗圃,其形状如直角梯形,有两边借用夹角为45°的两面墙,如图,另外两边是总长为30m的铁栅栏.
校园要建苗圃,其形状如直角梯形,有两边借用夹角为45°的两面墙,如图,另外两边是总长为30m的铁栅栏. 如图,已知二次函数的顶点坐标为D(-1,-8),与y轴交于点C(0,-6),与x轴交于A、B两点,求△ABC的面积.
如图,已知二次函数的顶点坐标为D(-1,-8),与y轴交于点C(0,-6),与x轴交于A、B两点,求△ABC的面积.