题目内容
12．下列各组数中，能构成直角三角形的是（ ）| A． | 1，$\sqrt{2}$，$\sqrt{3}$ | B． | 4，5，6 | C． | 6，8，11 | D． | 5，12，20 |
分析 判断是否为直角三角形，只要验证两小边的平方和等于最长边的平方即可．
解答 解：A、12+（$\sqrt{2}$）2=（$\sqrt{3}$）2，故是直角三角形，符合题意；
B、42+52=41≠62，故不是直角三角形，不符合题意；
C、62+82=100≠112，故不是直角三角形，不符合题意；
D、52+122=169≠202，故不是直角三角形，不符合题意．
故选A．
点评 本题考查勾股定理的逆定理的应用．判断三角形是否为直角三角形，已知三角形三边的长，只要利用勾股定理的逆定理加以判断即可．
练习册系列答案
相关题目
2．二次根式是最简二次根式的为（ ）
| A． | $3\sqrt{2x}$ | B． | $\sqrt{a^3}$ | C． | $\sqrt{8b}$ | D． | $\sqrt{\frac{y}{4}}$ |
17．一个正六边形的外接圆的半径为$\sqrt{2}$，则此正六边形的面积为（ ）
| A． | 3$\sqrt{3}$ | B． | $\frac{3\sqrt{3}}{2}$ | C． | $\frac{2\sqrt{2}}{3}$ | D． | 3$\sqrt{2}$ |
如图，O为坐标原点，⊙O的半径为1，点P是直线y=-2x-6上的动点，过点P作⊙O的切线PA、PB，A、B为切点，连接OA、OB，则四边形OAPB的面积的最小值为$\frac{\sqrt{155}}{5}$．
如图所示，在△ABC中，D是BC上一点，E，F，G，H分别是BD，BC，AC，AD的中点，请你探究EG，HF的位置关系，并说明理由．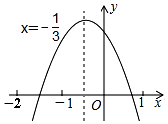
如图是二次函数y=ax2+bx+c（a≠0）的图象，有下列结论：①ab＞0；②a+b+c＜0；③b+2c＜0；④a-2b+4c＞0；⑤a=$\frac{3}{2}$b．其中正确的有（ ）