题目内容
19. 如图,已知等腰三角形△ABC,底角∠B=40°,CE是∠ACB的平分线,D是底边BC上一点,满足∠CAD=20°,若EF=1,则BE=1.
如图,已知等腰三角形△ABC,底角∠B=40°,CE是∠ACB的平分线,D是底边BC上一点,满足∠CAD=20°,若EF=1,则BE=1.
分析 在BC上取一点M,使CM=AC,连接EM,根据等腰三角形△ABC,底角∠B=40°得出∠BAC=100°,进一步得出∠EAF=100°-20°=80°,∠AEF=180°-100°-20°=60°,通过证得△ACE≌△MCE,得出AE=ME,∠CME=∠BAC=100°,∠AEF=∠CEM=60°从而得出∠EMB=EAF=80°,∠BEM=∠AEF=60°,根据ASA证得△AEF≌△MEB,得出EB=EF=1.
解答  解:在BC上取一点M,使CM=AC,连接EM,
解:在BC上取一点M,使CM=AC,连接EM,
∵等腰三角形△ABC,底角∠B=40°,
∴∠BAC=100°,∠ACB=∠B=40°,
∵CE是∠ACB的平分线,
∴∠ACE=∠BCE=20°,
∵∠CAD=20°,
∴∠EAF=100°-20°=80°,∠AEF=180°-100°-20°=60°,
在△ACE和△MCE中
$\left\{\begin{array}{l}{AC=MC}\\{∠ACE=∠MCE}\\{CE=CE}\end{array}\right.$
∴△ACE≌△MCE(SAS),
∴AE=ME,∠CME=∠BAC=100°,∠AEF=∠CEM=60°,
∴∠EMB=80°,∠BEM=60°,
∴∠EMB=EAF=80°,∠BEM=∠AEF=60°,
在△AEF和△MEB中,
$\left\{\begin{array}{l}{∠AEF=∠MEB}\\{AE=EM}\\{∠EAF=∠EMB}\end{array}\right.$,
∴△AEF≌△MEB(ASA),
∴EB=EF=1,
故答案为1.
点评 本题考查了等腰直角三角形的性质,三角形外角的性质,三角形内角和定理,平角的定义,作出辅助线构建全等三角形是解题的关键.

练习册系列答案
相关题目
9.下列式子中是一元一次不等式的是( )
| A. | -2>-5 | B. | x2>4 | C. | xy>0 | D. | $\frac{x}{2}$+x<-12 |
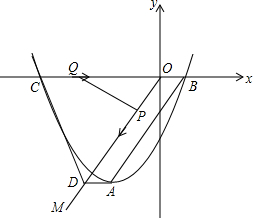 如图,顶点为A的抛物线y=a(x+2)2-4交x轴于点B(1,0),连接AB,过原点O作射线OM∥AB,过点A作AD∥x轴交OM于点D,点C为抛物线与x轴的另一个交点,连接CD.
如图,顶点为A的抛物线y=a(x+2)2-4交x轴于点B(1,0),连接AB,过原点O作射线OM∥AB,过点A作AD∥x轴交OM于点D,点C为抛物线与x轴的另一个交点,连接CD.
 如图,∠OBC=∠OCB,∠AOB=∠AOC,证明:△ABC是等腰三角形.
如图,∠OBC=∠OCB,∠AOB=∠AOC,证明:△ABC是等腰三角形.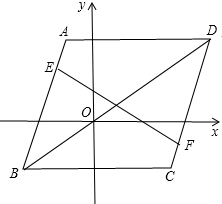 如图,在平面直角坐标系中,A(-1,3),B(-3,-2),C(3,-2),D(5,3),AB=CD,点E、F分别在AB、CD上,试判断∠BEF和∠DFE的大小关系并说明理由(提示:连接BD,先证明AB∥CD).
如图,在平面直角坐标系中,A(-1,3),B(-3,-2),C(3,-2),D(5,3),AB=CD,点E、F分别在AB、CD上,试判断∠BEF和∠DFE的大小关系并说明理由(提示:连接BD,先证明AB∥CD).