题目内容
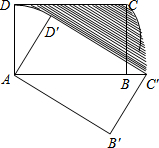 如图,在矩形ABCD中,AB=
如图,在矩形ABCD中,AB=| 3 |
考点:扇形面积的计算,旋转的性质
专题:
分析:根据图示知,S阴影=S扇形ACC′-S△AEC′+(
S矩形ABCD-S扇形ADD′-S△AD′E).根据图形的面积公式、旋转的性质以及勾股定理求得相关数据代入即可求得阴影部分的面积.
| 1 |
| 2 |
解答: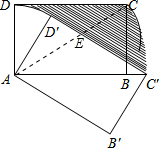 解:如图,连接AC.
解:如图,连接AC.
在矩形ABCD中,AB=CD=
,AD=1,则AC=
=2.
根据旋转的性质得到:∠DAD′=∠CAC′=α,AD=AD′=1,C′D′=CD=
.
所以 S阴影=S扇形ACC′-S△AEC′+(
S矩形ABCD-S扇形ADD′-S△AD′E)
=S扇形ACC′-S△AC′D′+
S矩形ABCD-S扇形ADD′,
=
-
×1×
+
×1×
-
=
.
故答案是:
.
 解:如图,连接AC.
解:如图,连接AC.在矩形ABCD中,AB=CD=
| 3 |
| AD2+CD2 |
根据旋转的性质得到:∠DAD′=∠CAC′=α,AD=AD′=1,C′D′=CD=
| 3 |
所以 S阴影=S扇形ACC′-S△AEC′+(
| 1 |
| 2 |
=S扇形ACC′-S△AC′D′+
| 1 |
| 2 |
=
| απ×22 |
| 360 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| απ×12 |
| 360 |
=
| πα |
| 120 |
故答案是:
| πα |
| 120 |
点评:此题主要考查了矩形的性质以及旋转的性质以及扇形面积公式等知识,此题利用了“分割法”对不规则图形进行面积的计算.

练习册系列答案
相关题目
如果单项式2am+2nbn-2m+2与a5b7是同类项,那么nm的值是( )
| A、-3 | ||
| B、-1 | ||
| C、3 | ||
D、
|
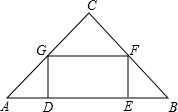 如图,在直角△ABC中,∠C=90°,矩形DEFG的四个顶点都在△ABC的边上,已知:AC=4,BC=3.
如图,在直角△ABC中,∠C=90°,矩形DEFG的四个顶点都在△ABC的边上,已知:AC=4,BC=3.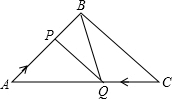 如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿着CA以每秒3cm的速度向A点运动,设运动时间为x秒.
如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿着CA以每秒3cm的速度向A点运动,设运动时间为x秒. 在Rt△ABC中,∠C=90°,b=5,c=5
在Rt△ABC中,∠C=90°,b=5,c=5 正方形ABCD边长为4,M,N分别是BC,CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直.
正方形ABCD边长为4,M,N分别是BC,CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直.