题目内容
13.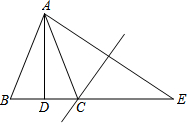 如图,等腰三角形ABC中,AB=AC,AD平分∠BAC,点E是线段BC延长线上一点,连接AE,点C在AE的垂直平分线上,若DE=10cm,则△ABC的周长等于20cm.
如图,等腰三角形ABC中,AB=AC,AD平分∠BAC,点E是线段BC延长线上一点,连接AE,点C在AE的垂直平分线上,若DE=10cm,则△ABC的周长等于20cm.
分析 根据线段垂直平分线上的点到线段两端点的距离相等可得AC=CE,根据等腰三角形三线合一的性质可得BD=CD,然后求出AB+BD=DE.
解答 解:∵点C在AE的垂直平分线上,
∴AC=CE,
∵AB=AC,AD平分∠BAC,
∴BD=CD,
∴AB+BD=AC+CD=CE+CD=DE,
∵DE=10cm,
∴AB+BC+AC=AB+BD+AC+CD=2×10=20cm,
即△ABC的周长等于20cm.
故答案为:20.
点评 本题考查了线段垂直平分线上的点到线段两端点的距离相等的性质,等腰三角形三线合一的性质,熟记性质并准确识图是解题的关键.

练习册系列答案
相关题目
1.下列四个数中,负数是( )
| A. | -3 | B. | 0 | C. | 1 | D. | 2 |
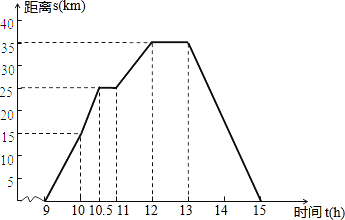 小明在某周末上午9时骑自行车离开家去绿道锻炼,15时回家,已知自行车离家的距离s(km)与时间t(h)之间的关系如图所示.根据图象回答下列问题:
小明在某周末上午9时骑自行车离开家去绿道锻炼,15时回家,已知自行车离家的距离s(km)与时间t(h)之间的关系如图所示.根据图象回答下列问题: