题目内容
8．已知：关于x的一元二次方程：x2+kx+3=0（1）当k=3时，判断方程根的情况；
（2）若方程的一个根是-1，求另一个根及k的值．
分析 （1）先求出△的值，再根据根的判别式即可得出方程根的情况；
（2）根据x1•x2=$\frac{c}{a}$和方程的一个根是-1，求出另一个根，再把其中的任意一根代入原方程，即可求出k的值．
解答 解：（1）∵当k=3时，△=32-4×1×3=-3＜0，
∴方程无解；
（2）∵x1x2=3，方程的一个根是-1，
∴-x2=-3，
把x1=-1代入x2+kx+3=0得：k=4，
则另一个根是-3，k的值是4．
点评 本题考查了一元二次方程ax2+bx+c=0（a≠0）的根与系数的关系：若方程的两根为x1，x2，则x1+x2=-$\frac{b}{a}$，x1•x2=$\frac{c}{a}$．也考查了一元二次方程的解．
练习册系列答案
相关题目
19．
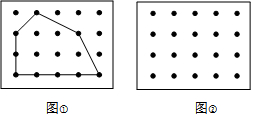图中有四个相邻点围成正方形面积是一个单位面积．在求图中点阵中多边形的面积时，你可以将多边形分割成若干个小正方形和三角形，分别计算面积后相加；或者你可能想到通过剪拼的方法计算．
（1）图①中多边形的面积8.5个平方单位；
（2）请你在图②中画一个面积为4.5个平方单位的多边形．在这个多边形内部的点数为3个，在这个多边形边界上的点数为5个．
（3）若设在这个多边形内部人点数为a个，多边形边界上的点数为b个，多边形的面积为S，可以借助下面的表格，猜想S，a，b之间的关系式．（S用关于a，b的代数式表示，直接写出结果，不用说明理由）．
图中有四个相邻点围成正方形面积是一个单位面积．在求图中点阵中多边形的面积时，你可以将多边形分割成若干个小正方形和三角形，分别计算面积后相加；或者你可能想到通过剪拼的方法计算．（1）图①中多边形的面积8.5个平方单位；
（2）请你在图②中画一个面积为4.5个平方单位的多边形．在这个多边形内部的点数为3个，在这个多边形边界上的点数为5个．
（3）若设在这个多边形内部人点数为a个，多边形边界上的点数为b个，多边形的面积为S，可以借助下面的表格，猜想S，a，b之间的关系式．（S用关于a，b的代数式表示，直接写出结果，不用说明理由）．
| a | $\frac{1}{2}b$ | S | S，a，b之间 的关系式 | |
| ① | ||||
| ② | 4.5 | |||
| … | … | … | … |
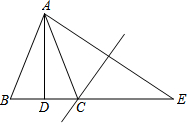如图，等腰三角形ABC中，AB=AC，AD平分∠BAC，点E是线段BC延长线上一点，连接AE，点C在AE的垂直平分线上，若DE=10cm，则△ABC的周长等于20cm．
如图，AB=AC=14cm，AB的垂直平分线交AB于点M，交AC于点 D，如果△DBC的周长是24cm，那么BC=10cm．