题目内容
5.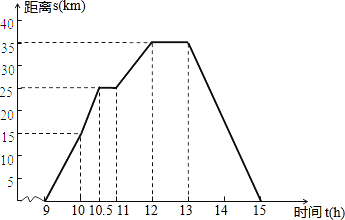 小明在某周末上午9时骑自行车离开家去绿道锻炼,15时回家,已知自行车离家的距离s(km)与时间t(h)之间的关系如图所示.根据图象回答下列问题:
小明在某周末上午9时骑自行车离开家去绿道锻炼,15时回家,已知自行车离家的距离s(km)与时间t(h)之间的关系如图所示.根据图象回答下列问题:(1)小明骑自行车离家的最远距离是35km;
(2)小明骑自行车行驶过程中,最快的车速是20km/h,最慢的车速是10km/h;
(3)途中小明共休息了2次,共休息了1.5小时;
(4)小明由离家最远的地方返回家时的平均速度是17.5km/h.
分析 (1)首先根据图象找到离家最远的距离,由此即可确定他到达离家最远的距离;
(2)根据图象可以直接看出纵坐标表示离家的距离,从横坐标中找到时间点,分别求出平均速度可直接得到答案;
(3)根据图象可以直接看出纵坐标表示离家的距离,从横坐标中找到时间点,即可得出答案;
(4)根据返回时所走路程和使用时间即可求出返回时的平均速度.
解答 解:(1)利用图象的纵坐标得出小明骑自行车离家的最远距离是35km;
故答案为:35;
(2)小明行驶中第一段行驶时间为;1小时,行驶距离为;15千米,故行驶速度为;15km/h,
小明行驶中第二段行驶时间为;0.5小时,行驶距离为;10千米,故行驶速度为;20km/h,
小明行驶中第三段行驶时间为;1小时,行驶距离为;10千米,故行驶速度为;15km/h,
故最快的车速是20km/h,最慢的车速是10km/h;
故答案为:20;10;
(3)根据图象得出有两段时间纵坐标标不变,得出途中小明共休息了2;利用横坐标得出休息时间为:1.5小时;
故答案为:1.5;
(4)∵返回时所走路程为35km,使用时间为2小时,
∴返回时的平均速度17.5km/h.
故答案为:17.5.
点评 此题主要考查了看函数图象,解决本题的关键是读懂图意,然后根据图象信息找到所需要的数量关系,利用数量关系即可解决问题.

练习册系列答案
相关题目
14.A、B两地相距135千米,两辆汽车均从A开往B,大汽车比小汽车早出发5小时,小汽车比大汽车早到30分钟,已知小汽车与大汽车的速度之比为5:2,若小汽车的速度为5x千米/小时,则可列方程为( )
| A. | $\frac{135}{2x}$=$\frac{135}{5x}$+5+$\frac{1}{2}$ | B. | $\frac{135}{2x}$=$\frac{135}{5x}$+5-$\frac{1}{2}$ | ||
| C. | $\frac{135}{5x}$=$\frac{135}{2x}$+5-$\frac{1}{2}$ | D. | $\frac{135}{5x}$=$\frac{135}{2x}$-5-$\frac{1}{2}$ |
15.若正方形的对角线长为2cm,则这个正方形的面积为( )
| A. | 4 cm2 | B. | 2 cm2 | C. | $\sqrt{2}$cm2 | D. | 2$\sqrt{2}$cm2 |
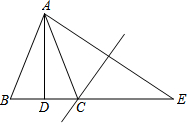 如图,等腰三角形ABC中,AB=AC,AD平分∠BAC,点E是线段BC延长线上一点,连接AE,点C在AE的垂直平分线上,若DE=10cm,则△ABC的周长等于20cm.
如图,等腰三角形ABC中,AB=AC,AD平分∠BAC,点E是线段BC延长线上一点,连接AE,点C在AE的垂直平分线上,若DE=10cm,则△ABC的周长等于20cm.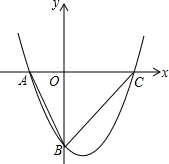 如图,抛物线y=x2-x-6交x轴于A、C两点,交y轴于点B;将抛物线y=x2-x-6向上平移$\frac{23}{4}$个单位长度、再向左平移m(m>0)个单位长度,得到新抛物线;若新抛物线的顶点P在△ABC内,则m的取值范围是0<m$<\frac{7}{3}$.
如图,抛物线y=x2-x-6交x轴于A、C两点,交y轴于点B;将抛物线y=x2-x-6向上平移$\frac{23}{4}$个单位长度、再向左平移m(m>0)个单位长度,得到新抛物线;若新抛物线的顶点P在△ABC内,则m的取值范围是0<m$<\frac{7}{3}$.