题目内容
3.若一次函数y=kx+b的图象经过点(0,3)和(-2,1),则此函数表达式为y=x+3.分析 将两点代入解析式中,然后列出方程组求出k与b的值.
解答 解:将(0,3)和(-2,1)代入y=kx+b
∴$\left\{\begin{array}{l}{3=b}\\{1=-2k+b}\end{array}\right.$
解得:$\left\{\begin{array}{l}{k=1}\\{b=3}\end{array}\right.$
∴函数的表达式为:y=x+3
故答案为:y=x+3
点评 本题考查一次函数解析式,解题的关键是将已知点的坐标代入解析式中,本题属于基础题型.

练习册系列答案
相关题目
14.A、B两地相距135千米,两辆汽车均从A开往B,大汽车比小汽车早出发5小时,小汽车比大汽车早到30分钟,已知小汽车与大汽车的速度之比为5:2,若小汽车的速度为5x千米/小时,则可列方程为( )
| A. | $\frac{135}{2x}$=$\frac{135}{5x}$+5+$\frac{1}{2}$ | B. | $\frac{135}{2x}$=$\frac{135}{5x}$+5-$\frac{1}{2}$ | ||
| C. | $\frac{135}{5x}$=$\frac{135}{2x}$+5-$\frac{1}{2}$ | D. | $\frac{135}{5x}$=$\frac{135}{2x}$-5-$\frac{1}{2}$ |
15.若正方形的对角线长为2cm,则这个正方形的面积为( )
| A. | 4 cm2 | B. | 2 cm2 | C. | $\sqrt{2}$cm2 | D. | 2$\sqrt{2}$cm2 |
12.下列从左到右的变形,属于因式分解的是( )
| A. | (x+1)(x-1)=x2-1 | B. | x2+2x=x(x+2) | C. | m2+m-4=m(m+1)-4 | D. | 2x2+2x=2x2(1+$\frac{1}{x}$) |
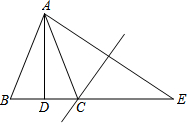 如图,等腰三角形ABC中,AB=AC,AD平分∠BAC,点E是线段BC延长线上一点,连接AE,点C在AE的垂直平分线上,若DE=10cm,则△ABC的周长等于20cm.
如图,等腰三角形ABC中,AB=AC,AD平分∠BAC,点E是线段BC延长线上一点,连接AE,点C在AE的垂直平分线上,若DE=10cm,则△ABC的周长等于20cm. 如图,AB=AC=14cm,AB的垂直平分线交AB于点M,交AC于点 D,如果△DBC的周长是24cm,那么BC=10cm.
如图,AB=AC=14cm,AB的垂直平分线交AB于点M,交AC于点 D,如果△DBC的周长是24cm,那么BC=10cm.