题目内容
17．若不等式组$\left\{\begin{array}{l}5-2x≤1\\ x-m＜0\end{array}\right.$只有2个整数解，则m的取值范围是3＜m≤4．分析 分别求出不等式组中不等式的解集，利用取解集的方法表示出不等式组的解集，根据解集中整数解有2个，即可得到m的范围．
解答 解：$\left\{\begin{array}{l}{5-2x≤1①}\\{x-m＜0②}\end{array}\right.$，
由①解得：x≥2，
由②解得：x＜m，
故不等式组的解集为2≤x＜m，
由不等式组的整数解有2个，得到整数解为2，3，
则m的范围为3＜m≤4．
故答案为3＜m≤4．
点评 此题考查了一元一次不等式组的整数解，表示出不等式组的解集，根据题意找出整数解是解本题的关键．
练习册系列答案
相关题目
（1）用数轴上的点表示下列各数：-5，2.5，3，-$\frac{5}{2}$，0，-|-3|，3$\frac{1}{2}$．
在△ABC中，AB=AC=4，∠A=α，P，Q分别是射线BA和AC延长线上的两点，且BP=CQ，连接PQ，与直线BC相交于点D，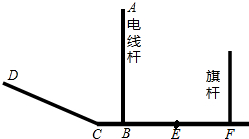
如图，CF为水平面，CD为坡面，线段EF为某一时刻旗杆在太阳光下的影子．