题目内容
13.已知抛物线y=-x2+mx+n经过点A(1,0),B(6,0).(1)求抛物线的解析式;
(2)当y<0,直接写出自变量x的取值范围;
(3)抛物线与y轴交于点D,P是x轴上一点,且△PAD是以AD为腰的等腰三角形,试求P点坐标.
分析 (1)把A点和B点坐标代入y=-x2+mx+n得到关于m、n的方程组,然后解方程组即可;
(2)先求出抛物线与x轴的交点坐标,然后写出抛物线在x轴上方所对应的自变量的范围即可;
(3)设P(t,0),先确定D(0,-6),利用勾股定理计算出AD=$\sqrt{37}$,再分类讨论:当DP=DA时,根据等腰三角形性质得点P与点A关于x轴对称,易得P点坐标为(-1,0);当AP=AD时,即AP=$\sqrt{37}$,再求粗OP的长,然后写出此时P点坐标.
解答 解:(1)根据题意得$\left\{\begin{array}{l}{-1+m+n=0}\\{-36+6m+n=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=7}\\{n=-6}\end{array}\right.$.
所以抛物线解析式为y=-x2+7x-6;
(2)当y=0时,-x2+7x-6=0,解得x1=1,x2=6,
所以当x<1或x>6时,y>0;
(3)设P(t,0)
当x=0时,y=-x2+7x-6=-6,则D(0,-6),
所以AD=$\sqrt{{1}^{2}+{6}^{2}}$=$\sqrt{37}$,
当DP=DA时,点P与点A关于x轴对称,此时P点坐标为(-1,0);
当AP=AD时,即AP=$\sqrt{37}$,则此时P点坐标为($\sqrt{37}$+1,0)或(-$\sqrt{37}$+1,0).
点评 本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

| A. | -4的平方根是±2 | B. | 0的平方根与算术平方根都是0 | ||
| C. | $\sqrt{16}$的平方根是±4 | D. | (-4)2的算术平方根是-4 |
| A. | 3 | B. | 2 | C. | -2 | D. | -3 |
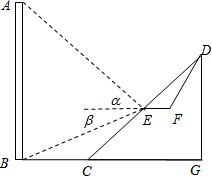 如图,高36米的楼房AB正对着斜坡CD,点E在斜坡CD的中点处,已知斜坡的坡角(即∠DCG)为30°,AB⊥BC.
如图,高36米的楼房AB正对着斜坡CD,点E在斜坡CD的中点处,已知斜坡的坡角(即∠DCG)为30°,AB⊥BC. 如图,AB∥CD,AE交CD于点C,DE⊥AE,垂足为E,∠A=37°,∠D=53°.
如图,AB∥CD,AE交CD于点C,DE⊥AE,垂足为E,∠A=37°,∠D=53°. 在△ABC中,AB=AC=4,∠A=α,P,Q分别是射线BA和AC延长线上的两点,且BP=CQ,连接PQ,与直线BC相交于点D,
在△ABC中,AB=AC=4,∠A=α,P,Q分别是射线BA和AC延长线上的两点,且BP=CQ,连接PQ,与直线BC相交于点D,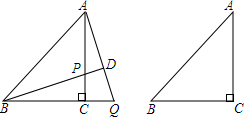 在△ABC中,BC=AC,∠BCA=90°,P为直线AC上一点,过A作AQ⊥BP于D,交直线BC于Q.
在△ABC中,BC=AC,∠BCA=90°,P为直线AC上一点,过A作AQ⊥BP于D,交直线BC于Q.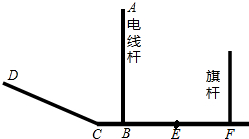 如图,CF为水平面,CD为坡面,线段EF为某一时刻旗杆在太阳光下的影子.
如图,CF为水平面,CD为坡面,线段EF为某一时刻旗杆在太阳光下的影子.