题目内容
11. 已知点A,B,C在⊙O上,且∠AOC=∠ABC=α,求α的值.
已知点A,B,C在⊙O上,且∠AOC=∠ABC=α,求α的值.
分析 设点E是优弧上一点,由圆周角定理可求∠AEC=$\frac{1}{2}$∠AOC=$\frac{1}{2}$α,由圆内接四边形的对角互补得出$\frac{1}{2}$α+α=180°,解方程即可.
解答  解:设点E是优弧上一点,
解:设点E是优弧上一点,
∵∠AOC=α,
∴∠AEC=$\frac{1}{2}$∠AOC=$\frac{1}{2}$α.
∵A,B,C,E四点共圆,
∴∠AEC+∠ABC=180°,即$\frac{1}{2}$α+α=180°,
解得α=120°.
点评 本题考查了圆内接四边形的性质:圆内接四边形的对角互补,也考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
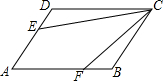 在平行四边形ABCD中,AB=10,AD=6,E是AD的中点,在AB上取一点F,使△CBF∽△CDE,则BF的长为$\frac{9}{5}$.
在平行四边形ABCD中,AB=10,AD=6,E是AD的中点,在AB上取一点F,使△CBF∽△CDE,则BF的长为$\frac{9}{5}$.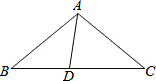 如图,在△ABC中,∠B=24°,∠C=30°,D为BC边上一点,AB=CD,连接AD,求证:△DBA∽△ABC.
如图,在△ABC中,∠B=24°,∠C=30°,D为BC边上一点,AB=CD,连接AD,求证:△DBA∽△ABC.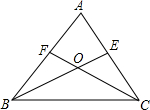 如图,BE、CF是△ABC的角平分线,BE、CF相交于点O.
如图,BE、CF是△ABC的角平分线,BE、CF相交于点O.
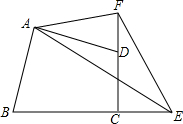 已知:四边形ABCD中,AB=AD,∠ABC+∠ADC=180°,E是BC的延长线上一点,F是CD的延长线上一点,∠BAD=2∠EAF,连结EF.求证:EF=BE-DF.
已知:四边形ABCD中,AB=AD,∠ABC+∠ADC=180°,E是BC的延长线上一点,F是CD的延长线上一点,∠BAD=2∠EAF,连结EF.求证:EF=BE-DF.