题目内容
1．
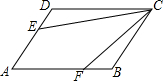在平行四边形ABCD中，AB=10，AD=6，E是AD的中点，在AB上取一点F，使△CBF∽△CDE，则BF的长为$\frac{9}{5}$．
分析 直接利用平行四边形的性质得出AE=DE=3，AB=DC=10，AB=BC=6，再利用相似三角形的性质得出答案．
解答 解：∵在平行四边形ABCD中，AB=10，AD=6，E是AD的中点，
∴AE=DE=3，AB=DC=10，AB=BC=6，
∵△CBF∽△CDE，
∴$\frac{BF}{DE}$=$\frac{BC}{DC}$，
∴$\frac{BF}{3}$=$\frac{6}{10}$，
解得：BF=$\frac{9}{5}$．
故答案为：$\frac{9}{5}$．
点评 此题主要考查了平行四边形的性质以及相似三角形的性质，熟练应用相似三角形的性质是解题关键．
练习册系列答案
相关题目
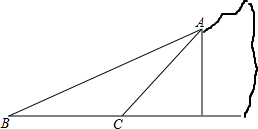因山体滑坡，需将一段50米长的滑坡体清除，滑坡体横截面是如图所示的△ABC．测得堡坎坡面AC的坡度是1：1，滑坡体坡面AB的坡角是30°，滑坡体底宽BC=13米．
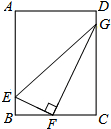如图，矩形ABCD中，E、G为AB、CD边上的点，F为BC的中点，且BE=1，CG=4，EF⊥FG．
在数轴上表示下列各数：2，-1，0，-$\frac{5}{4}$，-3.5，3，并用“＜”将它们连接起来．
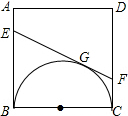如图，正方形ABCD的边长为a，以BC为直径向正方形内画半圆，EF切半圆于点G，分别交AB、CD于点E、F．
已知点A，B，C在⊙O上，且∠AOC=∠ABC=α，求α的值．