题目内容
16.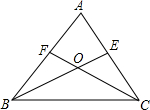 如图,BE、CF是△ABC的角平分线,BE、CF相交于点O.
如图,BE、CF是△ABC的角平分线,BE、CF相交于点O.(1)若∠ABC=50°,∠ACB=60°,求∠BOC的度数;
(2)若∠ABC+∠ACB=100°,求∠B0C的度数;
(3)若∠A=n°,你能否用含n的式子表示∠BOC的度数?若能,请直接写出来;若不能,请说明理由.
分析 (1)由∠ABC=50°,∠ACB=60°,BE、CF是△ABC的角平分线,可以求得∠OBC和∠OCB的度数,从而求出∠BOC的度数.
(2)由∠ABC+∠ACB=100°,BE、CF是△ABC的角平分线,可以求得∠OBC+∠OCB的度数,从而求出∠BOC的度数.
(3)根据三角形内角和等于180°,∠A=n°,从而可知∠ABC+∠ACB的度数,进而求得∠OBC+∠OCB的度数,从而求出∠BOC的度数.
解答 解:(1)∵∠ABC=50°,∠ACB=60°,BE、CF是△ABC的角平分线.
∴∠OBC=25°,∠OCB=30°.
又∵∠OBC+∠OCB+∠BOC=180°.
∴∠BOC=125°.
(2)∵∠ABC+∠ACB=100°,BE、CF是△ABC的角平分线.
∴∠OBC+∠OCB=50°.
又∵∠OBC+∠OCB+∠BOC=180°.
∴∠BOC=130°.
(3)能用含n的式子表示∠BOC的度数,∠BOC=90°$+\frac{1}{2}n°$.
∵∠A+∠ABC+∠ACB=180°,∠A=n°.
∴∠ABC+∠ACB=180°-n°.
又∵BE、CF是△ABC的角平分线.
∴∠OBC+∠OCB=$\frac{1}{2}(180°-n°)$=$90°-\frac{1}{2}n°$.
又∵∠OBC+∠OCB+∠BOC=180°.
∴∠BOC=180°-(∠OBC+∠OCB)=180°-($90°-\frac{1}{2}n°$)=180°-90°+$\frac{1}{2}n°$=$90°+\frac{1}{2}n°$.
即∠BOC=90°$+\frac{1}{2}n°$.
点评 本题考查三角形内角和的相关知识、运用角平分线的性质进行解答问题.关键是根据问题,进行灵活变化,对问题进行解答.

| A. | 10月2日21时 | B. | 10月2日7时 | C. | 10月2日5时 | D. | 10月1日7时 |
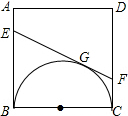 如图,正方形ABCD的边长为a,以BC为直径向正方形内画半圆,EF切半圆于点G,分别交AB、CD于点E、F.
如图,正方形ABCD的边长为a,以BC为直径向正方形内画半圆,EF切半圆于点G,分别交AB、CD于点E、F.
 已知:如图,在Rt△ABC中,∠B=90°,AB=5,BC=12,AC的垂直平分线与AC,BC分别交于点D,E.求:DE的长.
已知:如图,在Rt△ABC中,∠B=90°,AB=5,BC=12,AC的垂直平分线与AC,BC分别交于点D,E.求:DE的长. 已知点A,B,C在⊙O上,且∠AOC=∠ABC=α,求α的值.
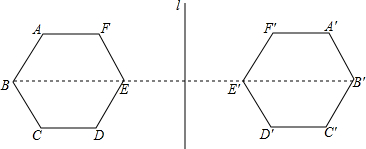
已知点A,B,C在⊙O上,且∠AOC=∠ABC=α,求α的值. 如图,把图形补成关于直线l对称的图形.
如图,把图形补成关于直线l对称的图形.