题目内容
20.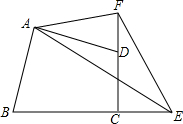 已知:四边形ABCD中,AB=AD,∠ABC+∠ADC=180°,E是BC的延长线上一点,F是CD的延长线上一点,∠BAD=2∠EAF,连结EF.求证:EF=BE-DF.
已知:四边形ABCD中,AB=AD,∠ABC+∠ADC=180°,E是BC的延长线上一点,F是CD的延长线上一点,∠BAD=2∠EAF,连结EF.求证:EF=BE-DF.
分析 在CB上截取BM=DF,连接AM,证△ABM≌△ADF,推出AF=AM,∠DAF=∠BAM,求出∠EAM=∠EAF,证△FAE≌△MAE,推出EF=EM即可.
解答  解:在CB上截取BM=DF,连接AM,
解:在CB上截取BM=DF,连接AM,
∵∠ABC+∠D=180°,∠ADC+∠ADF=180°,
∴∠ABC=∠ADF,
在△ABM和△ADF中$\left\{\begin{array}{l}{AB=AD}\\{∠B=∠ADF}\\{BM=DF}\end{array}\right.$,
∴△ABM≌△ADF(SAS),
∴AF=AM,∠DAF=∠BAM,
∵∠BAD=2∠EAF=2(∠EAD+∠DAF)=2(∠EAD+∠BAM)=∠EAF+(∠EAD+∠BAM),
又∵∠BAD=(∠BAM+∠EAD)+∠MAE,
∴∠MAE=∠EAF,
在△FAE和△MAE中,
$\left\{\begin{array}{l}{AE=AE}\\{∠FAE=∠MAE}\\{AF=AM}\end{array}\right.$,
∴△FAE≌△MAE(SAS),
∴EF=EM=BE-BM=BE-DF,
即EF=BE-DF.
点评 本题考查了全等三角形的性质和判定的应用,解此题的关键是能正确作辅助线,掌握全等三角形的判定方法.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
 已知点A,B,C在⊙O上,且∠AOC=∠ABC=α,求α的值.
已知点A,B,C在⊙O上,且∠AOC=∠ABC=α,求α的值. 如图,把图形补成关于直线l对称的图形.
如图,把图形补成关于直线l对称的图形.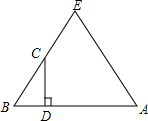 如图,△ABC是等边三角形,C为BE的中点,CD⊥AB于D,求$\frac{BD}{AD}$的值.
如图,△ABC是等边三角形,C为BE的中点,CD⊥AB于D,求$\frac{BD}{AD}$的值.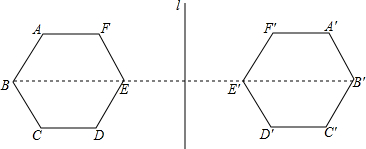
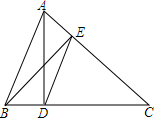 如图:AD和BE是锐角三角形ABC边BC、AC的两条高,垂足分别是点D和点E,若AC=6,CD=4,AB=5,求DE的长.
如图:AD和BE是锐角三角形ABC边BC、AC的两条高,垂足分别是点D和点E,若AC=6,CD=4,AB=5,求DE的长.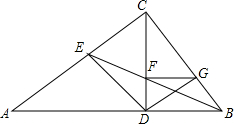 如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,∠ABC平分线交边AC于点E,交CD于F,过点F作FG∥AB,交边BC于点G,连结ED,GD.求证:$\frac{CE}{CD}$=$\frac{BG}{BD}$.
如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,∠ABC平分线交边AC于点E,交CD于F,过点F作FG∥AB,交边BC于点G,连结ED,GD.求证:$\frac{CE}{CD}$=$\frac{BG}{BD}$. 的解集在数轴上表示为( )
的解集在数轴上表示为( ) B.
B. 
 D.
D. 