题目内容
8.解方程与不等式.(1)$\frac{x}{3}+\frac{x-3}{2}$>1;
(2)$\frac{x}{x-1}-\frac{2}{x}$=1;
(3)解不等式组:$\left\{\begin{array}{l}{2x+5≤3(x+2)}\\{\frac{x-1}{2}<\frac{x}{3}}\end{array}\right.$.
分析 (1)先去分母,再去括号,移项、合并同类项,把x的系数化为1即可.
(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
(3)先求出两个不等式的解集,再求其公共解.
解答 解:(1)去分母得,2x+3(x-3)>6,
去括号得,2x+3x-9>6,
移项得,2x+3x>6+9,
合并同类项得,5x>15,
把x的系数化为1得,x>3.
(2)去分母得x2-2x+2=x2-x,
移项合并得:-x=-2,
解得:x=2,
经检验x=2是分式方程的解.
(3)$\left\{\begin{array}{l}{2x+5≤3(x+2)①}\\{\frac{x-1}{2}<\frac{x}{3}②}\end{array}\right.$
解不等式①,得x≥-1.
解不等式②,得x<3.
∴原不等式组的解集是-1≤x<3.
点评 此题考查了解分式方程和解不等式(组),解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.求不等式组解集的口诀:同大取大,同小取小,大小小大中间找,大大小小找不到.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
16.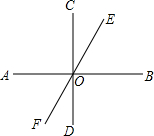 如图所示,直线AB,CD,EF相交于点O,且AB⊥CD于点O,∠BOE=70°,则∠FOD等于( )
如图所示,直线AB,CD,EF相交于点O,且AB⊥CD于点O,∠BOE=70°,则∠FOD等于( )
 如图所示,直线AB,CD,EF相交于点O,且AB⊥CD于点O,∠BOE=70°,则∠FOD等于( )
如图所示,直线AB,CD,EF相交于点O,且AB⊥CD于点O,∠BOE=70°,则∠FOD等于( )| A. | 10° | B. | 20° | C. | 30° | D. | 40° |
3. 如图,在?ABCD中,∠B=50°,CE平分∠BCD,交AD于E,则∠DCE等于( )
如图,在?ABCD中,∠B=50°,CE平分∠BCD,交AD于E,则∠DCE等于( )
 如图,在?ABCD中,∠B=50°,CE平分∠BCD,交AD于E,则∠DCE等于( )
如图,在?ABCD中,∠B=50°,CE平分∠BCD,交AD于E,则∠DCE等于( )| A. | 25° | B. | 40° | C. | 50° | D. | 65° |
18.班长在用计算器计算全班同学期中考试数学成绩,如果他不小心遗漏了一个最低的分数,那么他计算出的结果跟实际结果相比较是( )
| A. | 偏大 | B. | 偏小 | C. | 不变 | D. | 无法确定大小 |
 如图,在△ABC中,AD,AE分别是△ABC的高和角平分线,若∠B=30°,∠C=50°.
如图,在△ABC中,AD,AE分别是△ABC的高和角平分线,若∠B=30°,∠C=50°.