题目内容
17. 如图,在△ABC中,AD,AE分别是△ABC的高和角平分线,若∠B=30°,∠C=50°.
如图,在△ABC中,AD,AE分别是△ABC的高和角平分线,若∠B=30°,∠C=50°.(1)求∠DAE的度数;
(2)试探究∠DAE与∠B,∠C之间的关系,写出你的结论(不必证明)
分析 (1)根据三角形内角和定理求出∠BAC,再根据角平分线的定义求出∠BAD,根据直角三角形两锐角互余求出∠DAE,然后求解即可;
(2)利用(1)中的数据关系直接得出答案即可.
解答 解:(1)∵∠B=30°,∠C=50°,
∴∠BAC=180°-∠B-∠C=100°,
∵AD是角平分线,
∴∠BAD=$\frac{1}{2}$∠BAC=$\frac{1}{2}$×100°=50°,
∵AE是高,
∴∠BAE=90°-∠B=90°-50°=40°,
∴∠DAE=∠BAE-∠BAD=40°-30°=10°.
(2)∠DAE=$\frac{1}{2}$(∠C-∠B).
点评 本题考查了三角形的内角和定理,三角形的角平分线、高线的定义,直角三角形两锐角互余的性质,熟记定理并准确识图是解题的关键.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
12.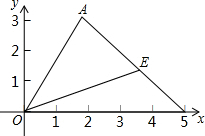 如图,在平面直角坐标系中,已知A(2,3),B(5,0),E(4,1),则三角形AOE的面积为( )
如图,在平面直角坐标系中,已知A(2,3),B(5,0),E(4,1),则三角形AOE的面积为( )
 如图,在平面直角坐标系中,已知A(2,3),B(5,0),E(4,1),则三角形AOE的面积为( )
如图,在平面直角坐标系中,已知A(2,3),B(5,0),E(4,1),则三角形AOE的面积为( )| A. | 5 | B. | 7.5 | C. | 10 | D. | 15 |
2.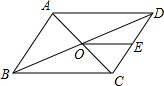 如图,?ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长是( )
如图,?ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长是( )
 如图,?ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长是( )
如图,?ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长是( )| A. | 24 | B. | 15 | C. | 21 | D. | 30 |
9.关于x的方程$\frac{2x-a}{x-1}$=1的解是正数,则a的取值范围是( )
| A. | a>-1 | B. | a>1且a≠2 | C. | a<-1 | D. | a<-1且a≠-2 |
16.以O(2,2)为圆心,3为半径作圆,则⊙O与直线y=kx+$\frac{1}{5}$k的位置关系是( )
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 都有可能 |