题目内容
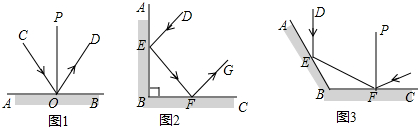
11.如图1,光线CO经过镜面AB反射得到光线OD,过点O作OP⊥AB,已知∠AOC=∠DOB.(1)求证:∠COP=∠DOP;
(2)如图2,若光线DE经取镜面AB和BC两次反射后得到光线FG,已知∠AED=∠BEF=α,∠EFB=∠GFC=β.
①若两镜面形成的夹角∠ABC=90°,求证:DE∥FG;
②如图3,若两镜面形成的夹角∠ABC=130°,过点F作PF⊥BC,且PF∥DE,求α和β的值.
分析 (1)先根据OP⊥AB得出∠AOE=∠BOE,再由∠AOC=∠DOB即可得出结论;
(2)①过点E作EP⊥AB,过点F作FH⊥BC,根据反射定律可知∠DEP=∠FEP,∠EFH=∠GFH,再由∠B=90°可知α+β=90°,再由∠BEF+∠FEP=90°,即α+∠FEP=90°,故∠FEP=β,再由∠AED=∠BEF=α可得出∠DEP=β,故∠DEF=2β.同理,∠EFG=2α,故∠DEF+∠EFG=180°,由此可得出结论;
②延长DE交CB的延长线于点G,根据补角的定义得出∠EBG的度数,由直角三角形的性质求出∠BEP的度数,根据对顶角相等得出α的值,由三角形内角和定理可得出β的值.
解答 (1)证明:∵OP⊥AB,
∴∠AOP=∠BOP=90°.
∵∠AOC=∠DOB,
∴∠COP=∠DOP;
(2)证明:①如图2,过点E作EP⊥AB,过点F作FH⊥BC,根据反射定律可知∠DEP=∠FEP,∠EFH=∠GFH,
∵∠B=90°,
∴∠BEF+∠BFE=90°,即α+β=90°.
∵∠BEF+∠FEP=90°,即α+∠FEP=90°,
∴∠FEP=β.
∵∠AED=∠BEF=α,∠DEP=β,
∴∠DEF=2β.
同理,∠EFG=2α,
∴∠DEF+∠EFG=180°,
∴DE∥FG;
②解:如图3,延长DE交CB的延长线与点G,
∵∠ABC=130°,
∴α=∠EBG=180°-130°=50°,
∴∠BEP=90°-50°=40°.
在△EBF中,β=180°-130°-40°=10°.
点评 本题考查的是平行线的判定与性质,熟知入射角等于反射角是解答此题的关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
12.下列几何体中,从上面看所得形状图不是四边形的是( )
| A. |  | B. |  | C. |  | D. |  |
10.小张上星期日买进某公司股票1000股,每股16元,下表为本周内每日该股票的涨跌情况(单位:元).根据你所学的数学知识,解答下列各题:
(1)星期四收盘每股是多少元?
(2)本周内最高价每股多少元?最低是每股多少元?
(3)小张买进股票时付0.15%的手续费,卖出时需付成交额0.15%的手续费和0.1%的交易税,如果小张在星期三收盘前将股票全部卖出,他的收益如何?
| 星 期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌 | +3 | -2.5 | +3.5 | -1.5 | -4 |
(2)本周内最高价每股多少元?最低是每股多少元?
(3)小张买进股票时付0.15%的手续费,卖出时需付成交额0.15%的手续费和0.1%的交易税,如果小张在星期三收盘前将股票全部卖出,他的收益如何?
 如图所示,?ABCD中,AE、CF分别平分∠BAD,∠BCD交DC、BA的延长线于E、F,求证:∠E=∠F.
如图所示,?ABCD中,AE、CF分别平分∠BAD,∠BCD交DC、BA的延长线于E、F,求证:∠E=∠F. 如图,在Rt△ABC中,∠BAC=90°,点D是BC的中点,且AD=AB,AB=2,求:
如图,在Rt△ABC中,∠BAC=90°,点D是BC的中点,且AD=AB,AB=2,求: 如图,已知直线AB、CD相交于点O,∠DOE=∠BOE,∠AOD=∠BOD+60°,求∠COE的度数.
如图,已知直线AB、CD相交于点O,∠DOE=∠BOE,∠AOD=∠BOD+60°,求∠COE的度数.