题目内容
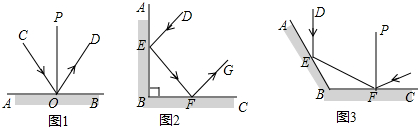
5.(1)观察图形1,根据图形面积的关系,不需要连其他的线,便可以得到一个乘法公式,这个公式是:(a+b)2=a2+2ab+b2.(2)有多张长方形卡片和正方形卡片(如图2):利用这些卡片,画出一个长方形,使它的面积为:2a2+3ab+b2.要求:画出卡片之间不能重叠.并根据这个长方形的面积写出一个代数恒等式.

分析 (1)本题根据几何图形来进行代数恒等式的推导,要注意图形各部分面积和=整个图形的面积.
(2)可使长方形的长为(2a+b),宽为(a+b)这样可以得到满足条件的等式.
解答 解:(1)(a+b)2=a2+2ab+b2;
(2)如图,
2a2+3ab+b2=(2a+b)(a+b).
点评 本题考查完全平方公式的几何背景,难度不大,注意利用几何图形推导代数恒等式,要注意几何图形整体面积与各部分面积的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.下列命题是真命题的是( )
| A. | 有两条边和一个角分别对应相等的两个三角形全等 | |
| B. | 两边分别相等的两个直角三角形全等 | |
| C. | 一个锐角和一条边分别相等的两个直角三角形全等 | |
| D. | 斜边和一个锐角分别相等的两个直角三角形全等 |
14.下列定理中,没有逆定理的是( )
| A. | 两直线平行,同旁内角互补 | |
| B. | 直角三角形的两个锐角互余 | |
| C. | 两个全等三角形的对应角相等 | |
| D. | 直角三角形中两直角边的平方和等于斜边的平方 |
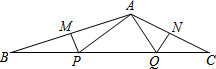 如图,∠BAC=130°,若MP和QN分别垂直平分AB和AC,则∠PAQ等于80°.
如图,∠BAC=130°,若MP和QN分别垂直平分AB和AC,则∠PAQ等于80°.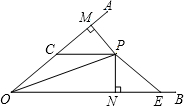 如图,OP平分∠AOB,∠AOB=40°,PM⊥OA于M,PN⊥OB于N,PC∥OB,交边OA于点C,E为边OB上的一点,且满足PC=PE.求∠EPN的度数?
如图,OP平分∠AOB,∠AOB=40°,PM⊥OA于M,PN⊥OB于N,PC∥OB,交边OA于点C,E为边OB上的一点,且满足PC=PE.求∠EPN的度数?