题目内容
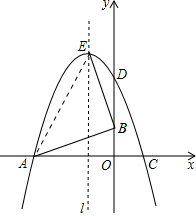
 如图,已知△OAB的顶点为A(-6,0),B(0,2),O是坐标原点,将△OAB绕点O按顺时针旋转90°,得到△ODC.
如图,已知△OAB的顶点为A(-6,0),B(0,2),O是坐标原点,将△OAB绕点O按顺时针旋转90°,得到△ODC.(1)写出C点的坐标为
(2)设过A,D,C三点的抛物线的解析式为y=ax2+bx+6,求其解析式;
(3)证明AB⊥BE.
考点:二次函数综合题
专题:
分析:(1)根据旋转的性质,可得OC=OB,进而可得C点的坐标;
(2)将A,C两点的坐标代入y=ax2+bx+6,利用待定系数法即可求出抛物线的解析式;
(3)已知A、B、E三点的坐标,运用两点间的距离公式计算得出AB2=40,BE2=40,AE2=80,则AB2+BE2=AE2,根据勾股定理的逆定理即可证明AB⊥BE.
(2)将A,C两点的坐标代入y=ax2+bx+6,利用待定系数法即可求出抛物线的解析式;
(3)已知A、B、E三点的坐标,运用两点间的距离公式计算得出AB2=40,BE2=40,AE2=80,则AB2+BE2=AE2,根据勾股定理的逆定理即可证明AB⊥BE.
解答:(1)解:∵将△OAB绕点O按顺时针旋转90°,得到△ODC,
∴△ODC≌△OAB,
∴OC=OB=2,
∴C点坐标为(2,0).
故答案为(2,0);
(2)解:∵抛物线y=ax2+bx+6过点A(-6,0),C(2,0),
∴
,
解得
,
 ∴抛物线的解析式为y=-
∴抛物线的解析式为y=-
x2-2x+6;
(3)证明:连接AE.
∵y=-
x2-2x+6=-
(x+2)2+8,
∴顶点E的坐标为(-2,8).
∵A(-6,0),B(0,2),E(-2,8),
∴AB2=62+22=40,BE2=(-2-0)2+(8-2)2=40,AE2=(-2+6)2+(8-0)2=80,
∴AB2+BE2=AE2,
∴AB⊥BE.
∴△ODC≌△OAB,
∴OC=OB=2,
∴C点坐标为(2,0).
故答案为(2,0);
(2)解:∵抛物线y=ax2+bx+6过点A(-6,0),C(2,0),
∴
|
解得
|
 ∴抛物线的解析式为y=-
∴抛物线的解析式为y=-| 1 |
| 2 |
(3)证明:连接AE.
∵y=-
| 1 |
| 2 |
| 1 |
| 2 |
∴顶点E的坐标为(-2,8).
∵A(-6,0),B(0,2),E(-2,8),
∴AB2=62+22=40,BE2=(-2-0)2+(8-2)2=40,AE2=(-2+6)2+(8-0)2=80,
∴AB2+BE2=AE2,
∴AB⊥BE.
点评:本题主要考查了旋转的性质,二次函数的解析式及顶点坐标的求法,勾股定理的逆定理,综合性较强,难度不大.运用待定系数法求二次函数的解析式是中考的常考点,需熟练掌握.

练习册系列答案
相关题目
 已知实数a、b、c在数轴上的位置如下,化简|a|+|b|+|a+b|-
已知实数a、b、c在数轴上的位置如下,化简|a|+|b|+|a+b|- 已知△ABC中,BC>AB>AC,∠ACB=40°,如果D、E是直线AB上的两点,且AD=AC,BE=BC,求∠DCE的度数.
已知△ABC中,BC>AB>AC,∠ACB=40°,如果D、E是直线AB上的两点,且AD=AC,BE=BC,求∠DCE的度数.
 如图所示,从A点到B点(只能从左向右,从上到下)共有
如图所示,从A点到B点(只能从左向右,从上到下)共有 如图,我国国旗上的五角星的每一个顶角都相等,其度数是
如图,我国国旗上的五角星的每一个顶角都相等,其度数是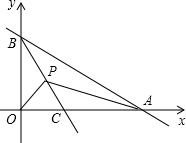 如图,A、B分别为x轴和y轴正半轴上的点.OA、OB的长分别是x2-14x+48=0的两根(OA>OB),直线BC平分∠ABO交x轴于C点,P为BC上一动点,P点以每秒1个单位的速度从B点开始沿BC方向向终点C移动
如图,A、B分别为x轴和y轴正半轴上的点.OA、OB的长分别是x2-14x+48=0的两根(OA>OB),直线BC平分∠ABO交x轴于C点,P为BC上一动点,P点以每秒1个单位的速度从B点开始沿BC方向向终点C移动