题目内容
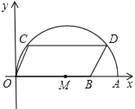
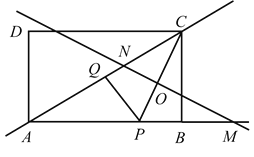
【题目】如图,矩形![]() 中,AB=8,BC=6,点
中,AB=8,BC=6,点![]() 是射线
是射线![]() 上一动点,设
上一动点,设![]() .过点
.过点![]() 做射线
做射线![]() 的垂线段
的垂线段![]() ,垂足为
,垂足为![]() ,作
,作![]() 的垂直平分线
的垂直平分线![]() 交射线
交射线![]() 于点
于点![]() ,交直线
,交直线![]() 于
于![]() .
.
![]() 点
点![]() 在边
在边![]() 上时.①用含
上时.①用含![]() 的代数式表示
的代数式表示![]() .②当
.②当![]() 时,直线ON交射线CD于
时,直线ON交射线CD于![]() ,求CE的长.
,求CE的长.
![]() 当
当![]() 为何值时,过
为何值时,过![]() 三点的圆与矩形
三点的圆与矩形![]() 的边或对角线
的边或对角线![]() 相切.
相切.
【答案】(1)①![]() ;②
;②![]() (2)当
(2)当![]() 为
为![]() 、
、![]() 或
或![]() 时,过
时,过![]() 、
、![]() 、
、![]() 三点的圆与矩形
三点的圆与矩形![]() 的边或对角线
的边或对角线![]() 相切
相切
【解析】
(1)①现根据勾股定理求得![]() ,然后设
,然后设![]() ,再由余弦函数得到
,再由余弦函数得到![]() ,两式相减即可得到答案;
,两式相减即可得到答案;
②先按比例分配求得![]() ,在由勾股定理求得
,在由勾股定理求得![]() ,然后根据线段垂直平分线的性质、相似三角形的判定和性质即可求得答案;
,然后根据线段垂直平分线的性质、相似三角形的判定和性质即可求得答案;
(2)对过![]() 三点的圆与矩形
三点的圆与矩形![]() 的边或对角线
的边或对角线![]() 相切进行分类讨论,分别画出图形并求得相应的
相切进行分类讨论,分别画出图形并求得相应的![]() 的值即可;
的值即可;
(1)①如图:

由矩形,AB=8,BC=6
可得 ![]()
∵![]() ,
,![]()
∴![]()
∴![]()
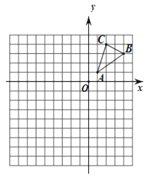
②如图:

∵当![]() :
:![]() =3:1时,
=3:1时,![]()
∴![]()
∵![]() 是
是![]() 的垂直平分线
的垂直平分线
∴![]()
∵![]() ,
,![]()
∴![]()
∴![]() 即
即![]()
∴![]() ;
;
(2) Ⅰ) 如图:

当⊙![]() 与边
与边![]() 相切于点
相切于点![]() 时,连结
时,连结![]()
∴![]()
∴![]()
∵![]()
∴![]()
∴![]()
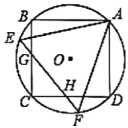
Ⅱ) 如图:
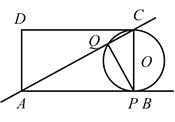
当![]() 与边
与边![]() 相切于点
相切于点![]() 时
时
点![]() 与点
与点![]() 重合,
重合,![]()
Ⅲ) 如图:

当⊙![]() 与对角线
与对角线![]() 相切于点
相切于点![]() 时
时
点![]() 与点
与点![]() 重合,
重合,![]()
∴![]()
∴综上所述,当![]() 为
为![]() 、
、![]() 或
或![]() 时,过
时,过![]() 、
、![]() 、
、![]() 三点的圆与矩形
三点的圆与矩形![]() 的边或对角线
的边或对角线![]() 相切.
相切.

练习册系列答案
相关题目