Question

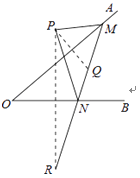
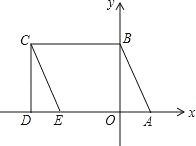
【题目】如图，在平面直角坐标系中，函数的图象经过点，直线与x轴交于点．

（1）求的值；

（2）过第二象限的点作平行于x轴的直线，交直线于点C，交函数的图象于点D．

①当时，判断线段PD与PC的数量关系，并说明理由；

②若，结合函数的图象，直接写出n的取值范围．

Answer 1

【答案】（1）．（2）①判断：．理由见解析；②或．

【解析】

（1）利用代点法可以求出参数 ；

（2）①当时，即点P的坐标为，即可求出点的坐标，于是得出；

②根据①中的情况，可知或再结合图像可以确定的取值范围；

解：（1）∵函数的图象经过点，

∴将点代入，即 ，得：

∵直线与轴交于点，

∴将点代入，即 ，得:

(2)①判断： ．理由如下：

当时，点P的坐标为，如图所示：

∴点C的坐标为 ，点D的坐标为

∴ ， ．

∴．

②由①可知当时

所以由图像可知，当直线往下平移的时也符合题意，即 ，

得；

当时，点P的坐标为

∴点C的坐标为 ，点D的坐标为

∴ ，

∴

当 时，即，也符合题意，

所以 的取值范围为：或 ．