题目内容
1. 已知四边形OABC是矩形,边OA在x轴上,边OC在y轴上,双曲线与边BC交于点D、与对角线OB交于点中点E,若△OBD的面积为10,则k的值是( )
已知四边形OABC是矩形,边OA在x轴上,边OC在y轴上,双曲线与边BC交于点D、与对角线OB交于点中点E,若△OBD的面积为10,则k的值是( )| A. | 10 | B. | 5 | C. | $\frac{10}{3}$ | D. | $\frac{20}{3}$ |
分析 设双曲线的解析式为:y=$\frac{k}{x}$,E点的坐标是(x,y),根据E是OB的中点,得到B点的坐标,求出点E的坐标,根据三角形的面积公式求出k.
解答 解:设双曲线的解析式为:y=$\frac{k}{x}$,E点的坐标是(x,y),
∵E是OB的中点,
∴B点的坐标是(2x,2y),
则D点的坐标是($\frac{k}{2y}$,2y),
∵△OBD的面积为10,
∴$\frac{1}{2}$×(2x-$\frac{k}{2y}$)×2y=10,
解得,k=$\frac{20}{3}$,
故选:D.
点评 本题考查反比例系数k的几何意义,过双曲线上的任意一点分别向两条坐标作垂线,与坐标轴围成的矩形面积就等于|k|.

练习册系列答案
相关题目
11.一直角三角形的斜边比一直角边大4,另一直角边长为8,则斜边长为( )
| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
16.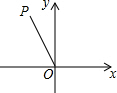 如图,已知∠POx=120°,OP=4,则点P的坐标是( )
如图,已知∠POx=120°,OP=4,则点P的坐标是( )
 如图,已知∠POx=120°,OP=4,则点P的坐标是( )
如图,已知∠POx=120°,OP=4,则点P的坐标是( )| A. | (2,4) | B. | (-2,4) | C. | (-2,2$\sqrt{3}$) | D. | (-2$\sqrt{3}$,2) |
6. 某公司招聘人才,共有50人进入复试.对应聘者分别进行阅读能力、思维能力和表达能力三项侧试,甲、乙两人的成绩如表(单位:分):
某公司招聘人才,共有50人进入复试.对应聘者分别进行阅读能力、思维能力和表达能力三项侧试,甲、乙两人的成绩如表(单位:分):
(1)根据实际需要,公司将阅读、思维和表达能力三项测试得分按3:5:2确定每人的最后成绩,若按此成绩在甲、乙两人中录用一人,谁将被录用?
(2)公司按照(1)中的成绩计算方法,将每位应聘者的最后成绩绘制成如图所示的频数分布直方图,请计算此次参加复试人员的平均分.
 某公司招聘人才,共有50人进入复试.对应聘者分别进行阅读能力、思维能力和表达能力三项侧试,甲、乙两人的成绩如表(单位:分):
某公司招聘人才,共有50人进入复试.对应聘者分别进行阅读能力、思维能力和表达能力三项侧试,甲、乙两人的成绩如表(单位:分):| 项目 人员 | 阅读 | 思维 | 表达 |
| 甲 | 93 | 86 | 73 |
| 乙 | 95 | 81 | 79 |
(2)公司按照(1)中的成绩计算方法,将每位应聘者的最后成绩绘制成如图所示的频数分布直方图,请计算此次参加复试人员的平均分.
10.分解因式a3-4a的结果是( )
| A. | a(a2-4) | B. | a(a+2)(a-2) | C. | a(a2+2)(a2-2) | D. | a(a2+4)(a2-4) |
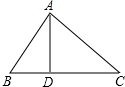 如图,在△ABC中,AB=15,AC=20,BC=25,AD是BC边上的高,
如图,在△ABC中,AB=15,AC=20,BC=25,AD是BC边上的高,