题目内容
10.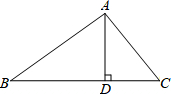 如图,在△ABC中,AD⊥BC,AB=5,BD=4,CD=$\sqrt{3}$.
如图,在△ABC中,AD⊥BC,AB=5,BD=4,CD=$\sqrt{3}$.(1)求AD的长.
(2)求△ABC的周长.
分析 (1)根据勾股定理求出AD;
(2)根据勾股定理求出AC,计算即可.
解答 解:(1)在Rt△ABD中,AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=3;
(2)在Rt△ACD中,AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=2$\sqrt{3}$,
则△ABC的周长=AB+AC+BC=5+4+$\sqrt{3}$+2$\sqrt{3}$=9+3$\sqrt{3}$.
点评 本题考查的是勾股定理,掌握直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2是解题的关键.

练习册系列答案
相关题目
1.下列各式中,不是最简二次根式的是( )
| A. | $\sqrt{8}$ | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
 如图,直线AB,CD相交于O,OE⊥AB,O为垂足,∠COE=34°,则∠BOD=56度.
如图,直线AB,CD相交于O,OE⊥AB,O为垂足,∠COE=34°,则∠BOD=56度.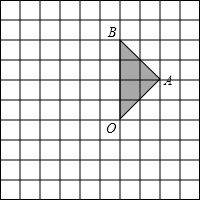 如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点,△ABO的三个顶点A、B、O都在格点上.
如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点,△ABO的三个顶点A、B、O都在格点上.