题目内容
函数y=mx+m和函数y=-mx2+2x+2(m是常数,且m≠0)的图象可能是( )
A、 |
B、 |
C、 |
D、 |
考点:二次函数的图象,一次函数的图象
专题:
分析:关键是m的正负的确定,对于二次函数y=ax2+bx+c,当a>0时,开口向上;当a<0时,开口向下.对称轴为x=-
,与y轴的交点坐标为(0,c).
| b |
| 2a |
解答:解:A.由函数y=mx+m的图象可知m<0,即函数y=-mx2+2x+2开口向上,与图象不符,故A选项错误;
B.由函数y=mx+m的图象可知m<0,即函数y=-mx2+2x+2开口向上,对称轴为x=-
=
<0,则对称轴应在y轴左侧,与图象不符,故B选项错误;
C.由函数y=mx+m的图象可知m>0,即函数y=-mx2+2x+2开口向下,与图象不符,故C选项错误;
D.由函数y=mx+m的图象可知m<0,即函数y=-mx2+2x+2开口向上,对称轴为x=-
=
<0,则对称轴应在y轴右侧,与图象相符,故D选项正确.
故选:D.
B.由函数y=mx+m的图象可知m<0,即函数y=-mx2+2x+2开口向上,对称轴为x=-
| b |
| 2a |
| 1 |
| m |
C.由函数y=mx+m的图象可知m>0,即函数y=-mx2+2x+2开口向下,与图象不符,故C选项错误;
D.由函数y=mx+m的图象可知m<0,即函数y=-mx2+2x+2开口向上,对称轴为x=-
| b |
| 2a |
| 1 |
| m |
故选:D.
点评:此题主要考查了一次函数和二次函数的图象性质以及分析能力和读图能力,要掌握它们的性质才能灵活解题.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
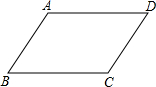 如图,已知在平行四边形ABCD中,AD=4cm,AB=3cm,则平行四边形ABCD的周长等于( )
如图,已知在平行四边形ABCD中,AD=4cm,AB=3cm,则平行四边形ABCD的周长等于( )| A、16cm | B、14cm |
| C、12cm | D、10cm |
下列各式:
①(-7)+(-7)=0;②(-3)2=-9;③(-2)3=-6;④-33=-27;⑤
=
.
其中运算正确的有( )
①(-7)+(-7)=0;②(-3)2=-9;③(-2)3=-6;④-33=-27;⑤
| 22 |
| 3 |
| 4 |
| 9 |
其中运算正确的有( )
| A、0个 | B、1个 | C、2个 | D、3个 |
在下列各数0,0.2,3π,
,6.1010010001…,
,
中,无理数的个数是( )
| 22 |
| 7 |
| 131 |
| 11 |
| 7 |
| A、1 | B、2 | C、3 | D、4 |
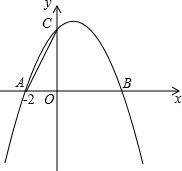 如图,已知抛物线y=ax2+bx+4与x轴交于A(-2,0)、B两点,与y轴交于C点,其对称轴为直线x=1.
如图,已知抛物线y=ax2+bx+4与x轴交于A(-2,0)、B两点,与y轴交于C点,其对称轴为直线x=1. 如图,小颖利用有一个锐角是45°的三角板测量一棵树的高度,已知她与树之间的水平距离BE为5米,小颖的眼睛距地面的距离AB为1.5米,求这棵树的高度.
如图,小颖利用有一个锐角是45°的三角板测量一棵树的高度,已知她与树之间的水平距离BE为5米,小颖的眼睛距地面的距离AB为1.5米,求这棵树的高度.